
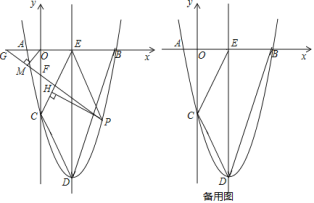
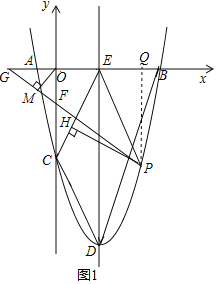
【题目】如图,在直角坐标系内,抛物线y=x2﹣4x﹣4与x轴交于点A,B,与y轴交于点C.顶点为D,对称轴与x轴的交点为E,连接BD,DC,CE.点P是抛物线在第四象限内一点,过点P作PH⊥CE,垂足为H.点F是y轴上一点,连接PF并延长交x轴于点G,过点O作OM⊥PG,垂足为M.
(1)当PH取得最大值时,求PE+PF+![]() OF的最小值;
OF的最小值;
(2)当PE+PF+![]() OF取得最小值时,把△OMF绕点O旋转a°(0<a≤360°),记旋转过程中的△OMF为△OM′F′.直线M′F′与x轴的交点为K.当△OF′K是以OK为底的等腰三角形时,直接写出所有满足条件的点M′的坐标.
OF取得最小值时,把△OMF绕点O旋转a°(0<a≤360°),记旋转过程中的△OMF为△OM′F′.直线M′F′与x轴的交点为K.当△OF′K是以OK为底的等腰三角形时,直接写出所有满足条件的点M′的坐标.
【答案】(1)PE+PF+![]() OF的最小值=5
OF的最小值=5![]() +
+![]() ;(2)点M′的坐标为:(﹣
;(2)点M′的坐标为:(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)先求得抛物线与坐标轴的交点坐标、顶点坐标,再待定系数法求直线CE解析式,再根据平行线一次项系数相等求经过点P且平行于CE的直线解析式,解方程组求点P坐标,求PE+PF+![]() OF最小值即求PF+
OF最小值即求PF+![]() OF的最小值,根据两点之间线段最短即可;
OF的最小值,根据两点之间线段最短即可;
(2)△OF′K是以OK为底的等腰三角形,按照顺时针旋转可分四种情形:①点M′在第三象限,OF′=KF′,点M′在第二象限,OF′=KF′,③点M′在第一象限,OF′=KF′,④点M′在第四象限,F′K=OF′;分别讨论即可.
解:(1)在抛物线y=x2﹣4x﹣4中,令x=0,则y=﹣4,∴C(0,﹣4),
令y=0,得x2﹣4x﹣4=0,解得:x1=2+2![]() ,x2=2﹣2
,x2=2﹣2![]() ,∴A(2﹣2
,∴A(2﹣2![]() ,0),B(2+2
,0),B(2+2![]() ,0)
,0)
∵y=x2﹣4x﹣4=(x﹣2)2﹣8,∴顶点D(2,﹣8),E(2,0),
易求得直线CE解析式为:y=2x﹣4,设经过点P且平行于CE的直线解析式为y=2x+b
由x2﹣4x﹣4=2x+b,得x2﹣6x﹣4﹣b=0,△=(﹣6)2﹣4(﹣4﹣b)=52+4b,
∵△=0时,点P到CE的距离PH最大,∴52+4b=0,即:b=﹣13
∴y=2x﹣13,解方程组![]() 得
得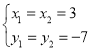
∴P(3,﹣7)
如图1,过点P作PQ⊥x轴于点Q,∵PE+PF+![]() OF中PE是定值,
OF中PE是定值,
∴PE+PF+![]() OF的最小即PF+
OF的最小即PF+![]() OF最小,令FM=
OF最小,令FM=![]() OF,则PF+
OF,则PF+![]() OF=PF+FM=PM
OF=PF+FM=PM
此时![]() =
=![]() ,∵∠OGF+∠GOM=∠GOM+∠FOM=90°
,∵∠OGF+∠GOM=∠GOM+∠FOM=90°
∴∠OGF=∠FOM,
∵∠FOG=∠FMO=90°
∴△FOG∽△FMO
∴![]() =
=![]() =
=![]()
∴![]() =
=![]()
∵△GPQ∽△GFO
∴![]() =
=![]() =
=![]()
∴QG=![]() ,
,
∴G(﹣![]() ,0)
,0)
∴PG=![]() ,GM=
,GM=![]()
∴PM=PG﹣GM=![]() ,
,
在△PEQ中,PE=![]() =
=![]() =5
=5![]()
∴PE+PF+![]() OF的最小值=5
OF的最小值=5![]() +
+![]() ;
;
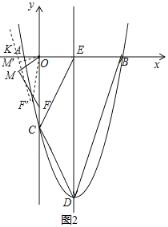
(2)①如图2,点M′在第三象限,∵△OF′K是以OK为底的等腰三角形,∴OF′=KF′=3,F′M′=![]()
∴M′K=KF′﹣F′M′=![]() ,
,
∴OK=![]() =
=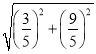 =
=![]() ,
,
设M′(m,n),则﹣nOK=KM′M′O
∴﹣![]() n=
n=![]() ×
×![]() ,解得:n=﹣
,解得:n=﹣![]() ,
,
∵tan∠KOM′=![]() =
=![]() ,即﹣
,即﹣![]() ×
×![]() =
=![]() m
m
∴m=﹣![]() ,
,
∴M′(﹣![]() ,﹣
,﹣![]() );
);
②如图3,点M′在第二象限,OF′=KF′,作F′H⊥x轴于H,作M′R⊥y轴于R,
∵OF′=KF′,F′H⊥x轴
∴OH=HK,
∵KM′=KF′+F′M′=3+![]() =
=![]() ,
,
∴OK=![]() =
=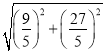 =
=![]()
∵∠ORM′=∠KM′O=90°,∠ROM′+∠KOM′=∠OKM′+∠KOM′=90°
∴∠ROM′=∠OKM′
∴△OM′R∽△KOM′
∴![]() =
=![]() =
=![]() ,即:
,即:![]() =
=![]() =
=![]()
∴M′R=![]() ,OR=
,OR=![]() ,
,
∴M′(﹣![]() ,
,![]() );
);
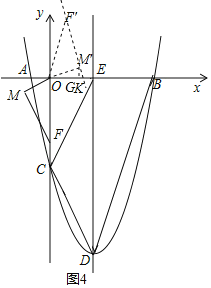
③如图4,作M′G⊥x轴于G,点M′在第一象限,OF′=KF′,∵F′O=F′K=3,M′K=3﹣![]() =
=![]() ,
,
∴OK=![]() =
=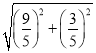 =
=![]() ,M′G=
,M′G=![]() =
=![]() =
=![]() ,
,
∵tan∠M′OK=![]() =
=![]() =
=![]() =
=![]()
∴OG=![]() ,
,
∴M′(![]() ,
,![]() );
);
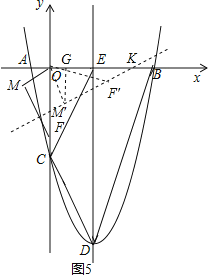
④如图5,点M′在第四象限,作M′G⊥x轴于G,∵F′K=OF′=3
∴M′K=M′F′+F′K=![]() +3=
+3=![]()
∴OK=![]() =
=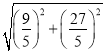 =
=![]()
∴M′G=![]() =
=![]() ,OG=
,OG=![]() =
=![]() ,
,
∴M′(![]() ,﹣
,﹣![]() );
);
综上所述,点M′的坐标为:(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
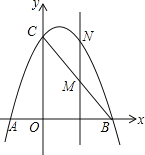
【题目】如图,已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0)两点,且交y轴交于点C.
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提倡节约用电,某地区规定每月用电量不超过 a 千瓦·时,居民生活用电基本价格为每千瓦时 0.5 元;若每月用电量超过 a 千瓦·时,则超过部分按基本电价提高 20%收费.居住此地的老李家二月份用电 120 千瓦·时,所交的电费为 66 元.
(1)求 a 的值;
(2)老李登录当地国家电网网络平台缴费后弹出一个对话框:您的家庭一月份和二月份的平均电费不超过0.54 元/千瓦·时,评为“节能小家庭”.试计算老李家一月份的用电量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元?
(2)为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
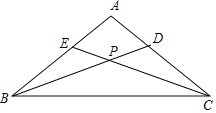
【题目】如图,在等腰△ABC中,AB=AC,CE、BD分别为∠ACB、∠ABC的角平分线,CE、BD相交于P.
(1)求证:CD=BE;
(2)若∠A=98°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
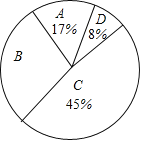
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在抛物线![]() 上,直线
上,直线![]() ⊥y轴于点M,AC⊥
⊥y轴于点M,AC⊥![]() 于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
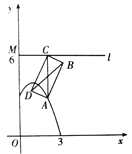
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列函数图象上任取不同两点P(x1,y1),Q(x2,y2),一定能使(x2﹣x1)(y2﹣y1)>0成立的是( )
A.y=﹣2x+1(x<0)B.y=﹣x2﹣2x+8(x<0)
C.y=![]() (x>0)D.y=2x2+x﹣6(x>0)
(x>0)D.y=2x2+x﹣6(x>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com