Question

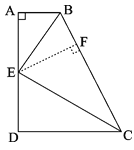
【题目】（1）如图，∠A=∠D=90°，BE平分∠ABC，且点E是AD的中点，求证：BC=AB+CD．

（2）如图，△ACB和△ECD都是等边三角形，点A、D、E在同一直线上，连接BE．

①求证：AD=BE；

②求∠AEB的度数．

Answer 1

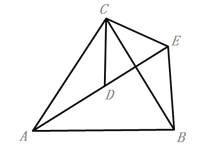
【答案】（1）证明见解析；（2）①证明见解析；②60°．

【解析】试题分析：（1）过点E作EF⊥BC于点F，可得∠EFB=∠A=90°，已知BE平分∠ABC，根据角平分线的定义可得∠ABE=∠FBE，利用AAS即可判定ΔABE≌ΔFBE，根据全等三角形的性质可得AE=EF，AB=BF，又由点E是AD的中点，可得AE=ED=EF，再利用HL判定RtΔCDE≌RtΔCFE，即可得CD=CF，所以BC=CF+BF=AB+CD；（2）①根据已知条件易证AC=BC，∠ACD=∠BCE，CD=CE，利用SAS证明△ACD≌△BCE，根据全等三角形的性质即可得AD=BE；②在等边△ECD中，∠CDE=∠CED=60°，即可得∠ADC=120°．

再由△ACD≌△BCE，根据全等三角形的对应边相等可得∠BEC=∠ADC=120°，所以∠AEB=∠BEC-∠CED=120°-60°=60°．

试题解析：

（1）过点E作EF⊥BC于点F，则∠EFB=∠A=90°

又∵BE平分∠ABC，∴∠ABE=∠FBE，∴ΔABE≌ΔFBE（AAS）

∴AE=EF，AB=BF，又点E是AD的中点， ∴AE=ED=EF

∴RtΔCDE≌RtΔCFE（HL）

∴CD=CF，∴BC=CF+BF=AB+CD

（2）①证明：∵△ACB和△ECD都是等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°

又∵∠ACD=∠ACB﹣∠DCB，∠BCE=∠DCE﹣∠DCB，∴∠ACD=∠BCE，在△ACD和△BCE中，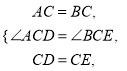

∴△ACD≌△BCE（SAS），∴AD=BE．

②在等边△ECD中，∠CDE=∠CED=60°，

∴∠ADC=120°．

∵△ACD≌△BCE，

∴∠BEC=∠ADC=120°，

∴∠AEB=∠BEC-∠CED=120°-60°=60°．