
分析 (1)由可获得利润p=-$\frac{1}{25}$(x-60)2+40(万元),即可知当x=60时,P最大,最大值为40,继而求得5年所获利润的最大值;
(2)首先求得前两年的获利最大值,注意前两年:0≤x≤50,此时因为P随x的增大而增大,所以x=50时,P值最大;然后后三年:设每年获利y,设当地投资额为a,则外地投资额为100-a,即可得函数y=P+Q=[-$\frac{1}{25}$(a-60)2+40]+{-$\frac{24}{25}$[100-(100-a)]2+$\frac{276}{5}$[100-(100-a)]+160},整理求解即可求得最大值,则可求得按规划实施,5年所获利润(扣除修路后)的最大值.
解答 解:(1)∵p=-$\frac{1}{25}$(x-60)2+40,
∴当x=60时,p取最大值40,
5年所获利润的最大值=40×5=200;
(2)∵a=-$\frac{1}{25}$<0,
∴当x<60时,p随x增大而增大,
∵拨出50万进行修路,
∴当地政府对该特产的销售投资为50万,
∴当x=50时,p取最大值,代入可得p=36,
则这两年在当地销售的最大利润=36×2=72;
后三年:设每年获利y,设当地投资额为a,则外地投资额为100-a,
∴y=P+Q=[-$\frac{1}{25}$(a-60)2+40]+{-$\frac{24}{25}$[100-(100-a)]2+$\frac{276}{5}$[100-(100-a)]+160}
=-a2+60a+56
=-(a-30)2+956,
∴当a=30时,y最大且为956,
∴这三年的获利最大为956×3=2868(万元),
∴5年所获利润(扣除修路后)的最大值是:72+2868-50×2=2840(万元).
点评 此题考查了二次函数的实际应用问题.解题的关键是理解题意,找到合适函数取得最大值,是解此题的关键,还要注意后三年的最大值的求解方法.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
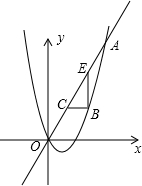 如图,已知抛物线y=$\frac{1}{2}$x2-x与直线y=2x交于O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E,以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
如图,已知抛物线y=$\frac{1}{2}$x2-x与直线y=2x交于O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E,以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
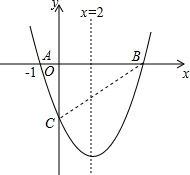 如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0),其顶点为D.
如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0),其顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
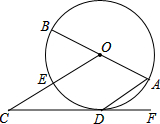 如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.
如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com