下列命题中.正确的是( )①顶点在圆周上的角是圆周角,②90°的圆周角所对的弦是直径,③圆周角度数等于圆心角度数的一半,④三点确定一个圆,⑤同弧所对的圆周角相等． A.①②③B.③④⑤C.②⑤D.②③ 题目和参考答案——青夏教育精英家教网—

下列命题中，正确的是（　　）
①顶点在圆周上的角是圆周角；②90°的圆周角所对的弦是直径；③圆周角度数等于圆心角度数的一半；④三点确定一个圆；⑤同弧所对的圆周角相等．

A、①②③	B、③④⑤
C、②⑤	D、②③

考点：命题与定理

专题：

分析：根据圆周角的定义对①进行判断；根据圆周角定理对②③⑤进行判断；根据确定圆的条件对④进行判断．

解答：解：顶点在圆周上且两边与圆相交的角是圆周角，所以①错误；
90°的圆周角所对的弦是直径，所以②正确；
在同圆或等圆中，同弧或等弧所对的圆周角度数等于它所对的圆心角度数的一半，所以③错误；
不共线的三点确定一个圆，所以④错误；同弧所对的圆周角相等，所以⑤正确．
故选C．

点评：本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

抛物线y=

x2+bx+c与y轴交于点C（O，一4），与x轴交于点A、B，且B点的坐标为（2，0）．
（1）求该抛物线的解析式；
（2）若点D为0A中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

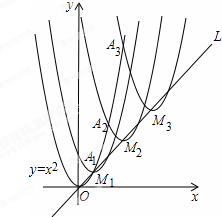如图，抛物线y=x²在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为A₁，A₂，A₃…A_n，…．将抛物线y=x²沿直线L：y=x向上平移，得一系列抛物线，且满足下列条件：
①抛物线的顶点M₁，M₂，M₃，…M_n，…都在直线L：y=x上；
②抛物线依次经过点A₁，A₂，A₃…A_n，…．
则顶点M₂₀₁₄的坐标为（　　）

A、（2013，2013）

B、（2014，2014）

C、（4027，4027）

D、（4028，4028）

查看答案和解析>>

科目：初中数学 来源： 题型：

二次函数y=x²的图象向左平移2个单位，得到新的图象的二次函数表达式是（　　）

A、y=x²+2

B、y=（x+2）²

C、y=（x-2）²

D、y=x²-2

查看答案和解析>>

科目：初中数学 来源： 题型：

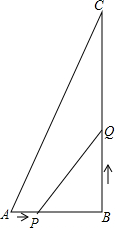如图所示，在△ABC中，∠B=90°，△ABC三边长为整数且两直角边的长为关于x的一元二次方程x²-7x+（2k+8）=0的两实数根，其中k为正整数，且AB＜BC．
（1）求△ABC的三边长；
（2）点P从A点开始沿AB边向点B以1个单位长/秒的速度移动，而点Q从B点开始沿BC边向C以2个单位长/秒的速度移动，如果P，Q分别从A，B同时出发，经过几秒钟，△PBQ的面积为△ABC面积的

？

查看答案和解析>>

科目：初中数学 来源： 题型：

下列关于抛物线y=x²-2x+1的说法中，正确的是（　　）

A、对称轴是x=-1

B、开口向下

C、与y轴的交点为（0，1）

D、顶点坐标为（1，1）

查看答案和解析>>

科目：初中数学 来源： 题型：

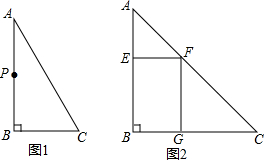【问题发现】
（1）如图①，△ABC为直角三角形，∠B=90°，P是边AB上任意一点（不写A、B重合），请你在△ABC的边长找另一点Q，使得S_△BCP=S_△BCQ，并简要说明方法；
（2）如图②，△ABC为等腰三角形，∠B=90°，AB=10，F是边AC上任意一点（不与A、C重合），EF⊥AB，FG⊥BC，试判断图中△AEF、△CGF、四边形BEFG的具体形状；（直接写出答案）．
【问题探究】
（3）在（2）的条件下研究：F在边长AC上移动时，四边形BEFG的周长是否发生改变，并说明理由；（不妨设AE=x）
（4）在（2）的条件下研究：F在边AC上移动时，四边形BEFG的面积是否存在最大值？若存在，求出来；若不存在，说明理由．（提示：我们知道完全平方式具有非负性，即（a+b）²≥0，显然（a+b）²有最小值．例如：对于y=x²+2x+2=（x+1）²+1≥1，那么y有最小值1）．

查看答案和解析>>

科目：初中数学 来源： 题型：