
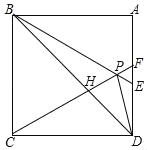
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是_____(填序号)
【答案】①②④
【解析】
由正方形的性质和相似三角形的判定与性质,即可得出结论.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠FDP=∠PBD=15°,∠ADB=45°,
∴∠PDB=30°,而∠DFP=60°,
∴∠PFD≠∠PDB,
∴△PFD与△PDB不会相似;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴![]() ,
,
∴DP2=PHPC,故④正确;
故答案是:①②④.


科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,点P是抛物线![]() 上的一个动点,点A的坐标为(0,-3).
上的一个动点,点A的坐标为(0,-3).
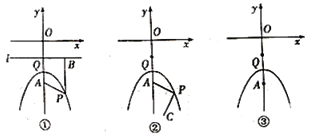
(1)如图①所示,直线l过点Q(0,-1)且平行于x轴,过P点作PB⊥l,垂足为B,连接PA,猜想PA与PB的大小关系,并证明你的猜想.
(2)请利用(1)的结论解决下列问题:
①如图②所示,设点C的坐标为(2,-5),连接PC,问PA+PC是否存在最小值?如果存在,请并求出点P的坐标;如果不存在,请说明理由.
②若过动点P和点Q(0,-1)的直线交抛物线于另一点D,且PA=4AD,求直线PQ的表达式(图③为备用图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
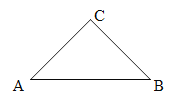
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4.
(1)尺规作图:将△ABC绕AC的中点O为旋转180°,点B的对应点为B′(保留作图痕迹,不写做法);
(2)求点B与点B′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
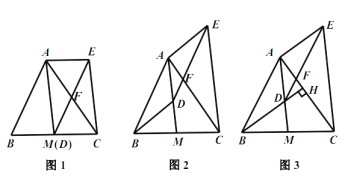
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形
是平行四边形
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
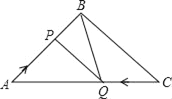
【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)x为何值时,PQ∥BC;
(2)是否存在某一时刻,使△APQ∽△CQB?若存在,求出此时AP的长;若不存在,请说明理由;
(3)当![]() =
=![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平面直角坐标系中的点A(a,1),t=ab﹣a2﹣b2(a,b是实数)
(1)若关于x的反比例函数y=![]() 过点A,求t的取值范围.
过点A,求t的取值范围.
(2)若关于x的一次函数y=bx过点A,求t的取值范围.
(3)若关于x的二次函数y=x2+bx+b2过点A,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
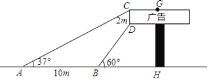
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com