
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
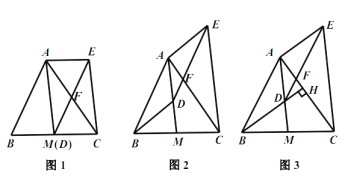
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形
是平行四边形
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求 ![]() 的长.
的长.
【答案】(1)证明见解析(2)成立,理由见解析;(3)①30°.②1+![]() .
.
【解析】
试题(1)只要证明AE=BM,AE∥BM即可解决问题;
(2)成立.如图2中,过点M作MG∥DE交CE于G.由四边形DMGE是平行四边形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,只要证明MI=![]() AM,MI⊥AC,即可解决问题;
AM,MI⊥AC,即可解决问题;
②设DH=x,则AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出![]() ,可得
,可得![]() ,解方程即可;
,解方程即可;
试题解析:(1)证明:如图1中,

∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,
∴四边形ABDE是平行四边形.
(2)结论:成立.理由如下:
如图2中,过点M作MG∥DE交CE于G.
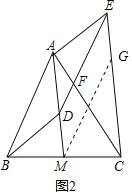
∵CE∥AM,
∴四边形DMGE是平行四边形,
∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(3)①如图3中,取线段HC的中点I,连接MI,
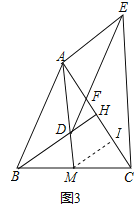
∵BM=MC,
∴MI是△BHC的中位线,
∴∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM.
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°.
②设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,
∴BH=4+2x,
∵四边形ABDE是平行四边形,
∴DF∥AB,
∴![]() ,
,
∴![]() ,
,
解得x=1+![]() 或1-
或1-![]() (舍弃),
(舍弃),
∴DH=1+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数的解析式为![]() .
.
(1)它与![]() 轴的交点的坐标为________,顶点坐标为________;
轴的交点的坐标为________,顶点坐标为________;
(2)在给定的坐标系中画出这个二次函数的图象,并求出抛物线与坐标轴的交点所组成的三角形的面积;
(3)根据图象直接写出抛物线在![]() 范围内,函数值
范围内,函数值![]() 的取值范围是________.
的取值范围是________.
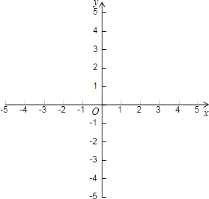
查看答案和解析>>
科目:初中数学 来源: 题型:
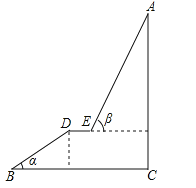
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
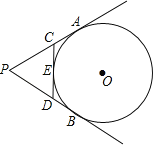
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
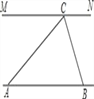
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行
河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,
沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
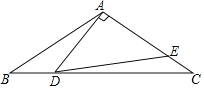
A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com