
【题目】如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是__.
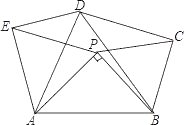
【答案】1.
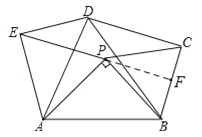
【解析】试题分析:先延长EP交BC于点F,得出PF⊥BC,再判定四边形CDEP为平行四边形,根据平行四边形的性质得出:四边形CDEP的面积=EP×CF=a×![]() b=
b=![]() ab,最后根据
ab,最后根据![]() ,判断
,判断![]() ab的最大值即可.
ab的最大值即可.
试题解析:延长EP交BC于点F,∵∠APB=90°,∠AOE=∠BPC=60°,∴∠EPC=150°,∴∠CPF=180°﹣150°=30°,∴PF平分∠BPC,又∵PB=PC,∴PF⊥BC,设Rt△ABP中,AP=a,BP=b,则
CF=![]() CP=
CP=![]() b,
b,![]() ,∵△APE和△ABD都是等边三角形,∴AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,∴△EAD≌△PAB(SAS),∴ED=PB=CP,同理可得:△APB≌△DCB(SAS),∴EP=AP=CP,∴四边形CDEP是平行四边形,∴四边形CDEP的面积=EP×CF=a×
,∵△APE和△ABD都是等边三角形,∴AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,∴△EAD≌△PAB(SAS),∴ED=PB=CP,同理可得:△APB≌△DCB(SAS),∴EP=AP=CP,∴四边形CDEP是平行四边形,∴四边形CDEP的面积=EP×CF=a×![]() b=
b=![]() ab,又∵
ab,又∵![]() ≥0,∴2ab≤
≥0,∴2ab≤![]() ,∴
,∴![]() ab≤1,即四边形PCDE面积的最大值为1.故答案为:1.
ab≤1,即四边形PCDE面积的最大值为1.故答案为:1.


科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点都在正方形网格的格点上,点
的顶点都在正方形网格的格点上,点![]()
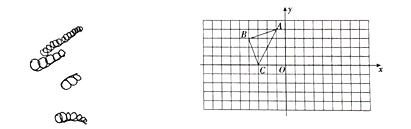
(1)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为___________.
的坐标为___________.
(2)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为__________.
的坐标为__________.
(3)观察图形,说一说点![]() 和点
和点![]() 的坐标有什么特点.
的坐标有什么特点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
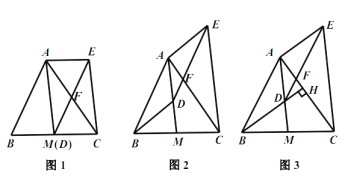
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形
是平行四边形
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
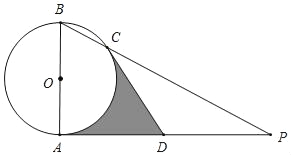
【题目】如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AB=2,∠P=30°,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com