
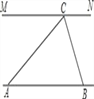
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行
河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,
沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
科目:初中数学 来源: 题型:
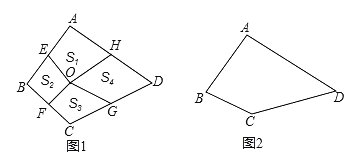
【题目】定义:我们把对角线互相垂直的四边形叫做和美四边形,对角线交点称为和美四边形的中心.
(1)写出一种你学过的和美四边形_________;
(2)如图1,点O是和美四边形ABCD的中心,E,F,G、H分别是边AB,BC,CD,DA的中点,连接OE,OF,OG,OH,记四边形AEOH,BEOF,CGOF,DHOG的面积为![]() ,用等式表示
,用等式表示![]() 的数量关系(无需说明理由).
的数量关系(无需说明理由).
(3)如图2,四边形ABCD是和美四边形,若AB=3,BC=2,CD=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.
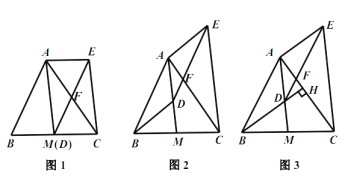
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形
是平行四边形
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
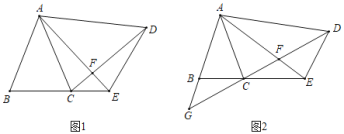
(1)求证:BE=CD.
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
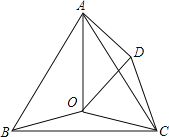
【题目】如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=m°,D是△ABC外一点,且△ADC≌△BOC,连接OD.当m为_____时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
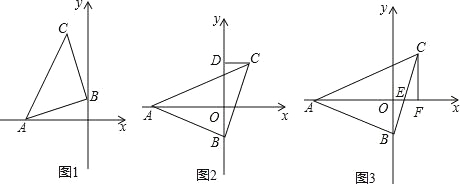
【题目】已知,△ABC 是等腰直角三角形,BC=AB,A 点在 x 负半轴上,直角顶点 B 在 y 轴上,点 C 在 x 轴上方.
(1)如图1所示,若A的坐标是(﹣3,0),点 B的坐标是(0,1),求点 C 的坐标;
(2)如图2,过点 C 作 CD⊥y 轴于 D,请直接写出线段OA,OD,CD之间等量关系;
(3)如图3,若 x 轴恰好平分∠BAC,BC与 x 轴交于点 E,过点 C作 CF⊥x 轴于 F,问 CF 与 AE 有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
球的类别 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com