Question

9．如图①，在△ABC中，∠A=90°，AB=AC，点D、E分别在AB、AC上，∠ADE=∠ABC．
初步感知：将图①中△ADE绕点A顺时针旋转α度，当α=180°时，如图②，易知△ABE和△ADC的面积相等．（不用证明）
深入探究：将图①中的△ADE绕点A顺时针α度，当0°＜α＜180°时，如图③，猜想△ABE和△ADC的面积之间的关系，并说明理由．
简单应用：将△ADE绕点A顺时针旋转α度，当AB=5，AD=3时，在旋转过程中，△ABE与△ADC面积的和达到的最大值为15．

Answer 1

分析 深入探究：作辅助线得到∠ANE=∠AMD=90°，再由旋转得到的结论判断出△ENA≌△DMA即可；
简单应用：根据旋转的过程中△ADE的面积始终保持不变，而在旋转的过程中，△ADC的AC始终保持不变，即可．

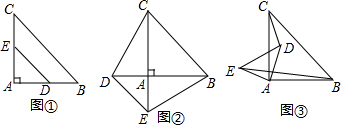
解答 初步感知
解：由旋转可知，∠DAC=∠EAB，AD=AE，AC=AB；
在△DAC和△EAB中，
$\left\{\begin{array}{l}{AD=AE}\\{∠DAC=∠EAB}\\{AC=AB}\end{array}\right.$，
∴△DAC≌△EAB，
∴S_△DAC=S_△EAB，
∴△ABE和△ADC的面积相等；
深入探究
解：△ABE和△ADC的面积相等；
理由如下：过点D作PM⊥AC，过点E作EN⊥AB，
∴∠ANE=∠AMD=90°，
由旋转有，∠EAD=∠CAB=90°，
∴∠EAM+∠DAM=90°，
∵∠EAN+∠EAM=90°，
∴∠EAN=∠DAM，
∵AE=AD，
∴△ENA≌△DMA，
∴EN=DM，
∵△ABE的面积为$\frac{1}{2}$AB×EN，△ADC的面积为$\frac{1}{2}$AC×DM，且AB=AC，
∴△ABE和△ADC的面积相等；
简单应用
如图

由旋转可知，在旋转的过程中△ADE的面积始终保持不变，
∴△ABE与△ADC面积的和达到的最大，
∴△ADC面积最大，
∵在旋转的过程中，AC始终保持不变，
∴要△ADC面积最大，
∴点D到AC的距离最大，
∴DA⊥AC，
∴△ABE与△ADC面积的和达到的最大为2×$\frac{1}{2}$×AC×AD=5×3=15，
故答案为15．

点评 此题是几何变换综合题，主要考查了旋转和全等三角形的性质和判定，旋转过程中面积变化分析，解本题的关键是三角形全等的判定．