
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 . 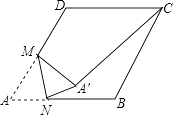
科目:初中数学 来源: 题型:
【题目】将样本容量为100的样本编制成组号①~⑧的八个组,简况如表所示:
组号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
频数 | 14 | 11 | 12 | 13 | ■ | 13 | 12 | 10 |
那么第⑤组的频率是( )
A. 14B. 15C. 0.14D. 0.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题 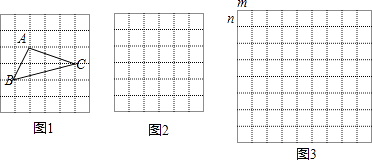
(1)在△ABC中,AB、BC、AC三边的长分别为 ![]() 、
、 ![]() 、
、 ![]() ,求这个三角形的面积. 如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.
,求这个三角形的面积. 如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.
请你将△ABC的面积直接填写在横线上 .
(2)思维拓展: 已知△ABC三边的长分别为 ![]() a(a>0),求这个三角形的面积.
a(a>0),求这个三角形的面积.
我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.
(3)类比创新: 若△ABC三边的长分别为 ![]() (m>0,n>0,且m≠n),求出这个三角形的面积.
(m>0,n>0,且m≠n),求出这个三角形的面积.
如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏本20元,而按标价的8折出售将赚40元.为了保证不亏本,最少要打 折( )
A. 6 B. 6.5 C. 7 D. 7.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
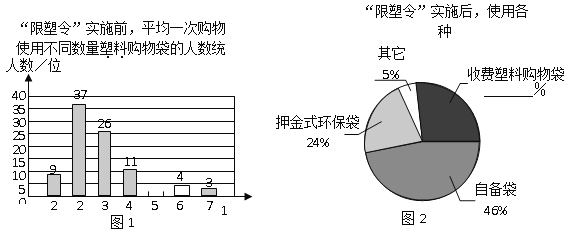
【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 总人数的百分比 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com