
����Ŀ������� 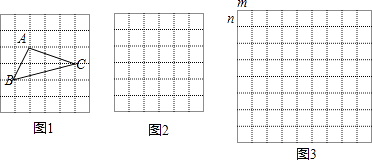
��1���ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ ![]() ��
�� ![]() ��
�� ![]() ������������ε������ ��ͼ1��ijͬѧ�ڽ�������ʱ���Ƚ���һ��ÿ��С�����εı߳�����1���������������л����߳�����Ҫ��ĸ��������ABC������ABC�������㶼��С�����εĶ��㴦������������Ҫ���ABC�ĸߣ�������������ܾ�������������
������������ε������ ��ͼ1��ijͬѧ�ڽ�������ʱ���Ƚ���һ��ÿ��С�����εı߳�����1���������������л����߳�����Ҫ��ĸ��������ABC������ABC�������㶼��С�����εĶ��㴦������������Ҫ���ABC�ĸߣ�������������ܾ�������������
���㽫��ABC�����ֱ����д�ں����� ��
��2��˼ά��չ�� ��֪��ABC���ߵij��ֱ�Ϊ ![]() a��a��0��������������ε������
a��a��0�������������������
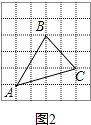
���ǰ��������ABC����ķ���������ͼ������ͼ2��������ÿ��С�����εı߳�����a�����������л�����Ӧ�ġ�ABC����������������
��3����ȴ��£� ����ABC���ߵij��ֱ�Ϊ ![]() ��m��0��n��0����m��n���������������ε������
��m��0��n��0����m��n��������������������
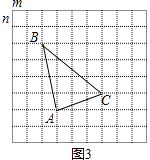
��ͼ3��������ÿ��С�����γ���������m��n�����������л�����Ӧ�ġ�ABC�������������������ε������
���𰸡�
��1���⣺��ABC�����=2��4�� ![]() ��1��2��
��1��2�� ![]() ��1��4��
��1��4�� ![]() ��1��3=3.5�� �ʴ�Ϊ��3.5
��1��3=3.5�� �ʴ�Ϊ��3.5
��2���⣺��ͼ2����ABC�����=3a��4a�� ![]() ��3a��2a��
��3a��2a�� ![]() ��a��4a��
��a��4a�� ![]() ��2a��2a=5a2
��2a��2a=5a2
��3���⣺��ͼ3����ABC�����=4m��4n�� ![]() ��m��4n��
��m��4n�� ![]() ��3m��n��
��3m��n�� ![]() ��4m��3n=6.5mn��
��4m��3n=6.5mn��
����������1�����ݾ��ε������ʽ�������ε������ʽ���㼴�ɣ���2�����ݹ��ɶ����������л�����Ӧ�ġ�ABC�����ݾ��ε������ʽ�������ε������ʽ��������������3�����ݹ��ɶ����������л�����Ӧ�ġ�ABC�����ݾ��ε������ʽ�������ε������ʽ������������
�����㾫����ͨ��������ù��ɶ����ĸ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����½��̻����2743000m2��2743000�ÿ�ѧ��������ʾΪ��������
A. 0.2743��107 B. 2.743��106 C. 27.43��105 D. 274.3��104
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2019��1��24�ա������ձ�����������ɽ��2018���������ͻ��86��Ԫ����86���ÿ�ѧ��������ʾΪ��������
A. 8.6��10B. 8.6��108C. 8.6��109D. 8.6��1010
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���D=90�㣬AB=2��BC=4��CD=AD= ![]() ��
�� 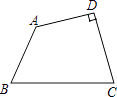
��1�����BAD����BCD�Ķ�����
��2�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2������ABCD�У���A=60�㣬M��AD�ߵ��е㣬N��AB���ϵ�һ���㣬����AMN��MN����ֱ�߷��۵õ���A��MN������A��C����A��C���ȵ���Сֵ�� �� 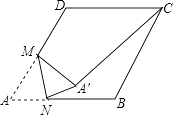
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���۵��ͷ�������ͼ����AO=BO=50cm��CO=DO=30cm�������ӷ�ƽ��ҪʹAB�������ĸ�Ϊ40cm��������������Ҫ�濪�ġ�AOBӦΪ�� �� 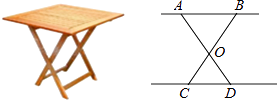
A.60��
B.90��
C.120��
D.150��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com