
【题目】△ABC是⊙O的内接三角形,BC= ![]() .如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=
.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA= ![]() BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 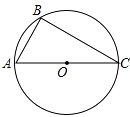
【答案】解:图形如图所示,直线l与⊙O相切. 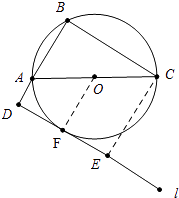
理由:作OF⊥l于F,CE⊥l于E,
∵AC是直径,
∴∠ABC=90°,
∵l⊥BD,
∴∠BDE=90°,
∵OF⊥l,CE⊥l,
∴AD∥OF∥CE,
∵AO=OC,
∴DF=FE,
∴OF= ![]() (AD+CE),
(AD+CE),
设AD=a,则AB=2AD=2a,
∵∠ABC=∠BDE=∠CED=90°,
∴四边形BDEC是矩形,
∴CE=BD=3a,
∴OF=2a,
∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2a,
∴AC=4a,
∴OF=OA=2a,
∴直线l是⊙O切线
【解析】作OF⊥l于F,CE⊥l于E,设AD=a,则AB=2AD=2a,只要证明OF是梯形ADEC的中位线即可解决问题.
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,若
中,若![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() 分别在
分别在![]() 和
和![]() 上,且
上,且![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
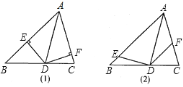
,垂足为![]() (如图
(如图![]() ),则可以得到以下两个结论:
),则可以得到以下两个结论:
①![]() ;②
;②![]() .
.
那么在![]() 中,仍然有条件“
中,仍然有条件“![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() ,分别在
,分别在![]() 和
和![]() 上”,请探究以下两个问题:
上”,请探究以下两个问题:
![]() 若
若![]() (如图
(如图![]() ),则
),则![]() 与
与![]() 是否仍相等?若仍相等,请证明;否则请举出反例.
是否仍相等?若仍相等,请证明;否则请举出反例.
![]() 若
若![]() ,则
,则![]() 是否成立?(只写出结论,不证明)
是否成立?(只写出结论,不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个. 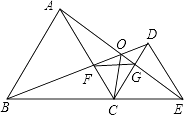
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
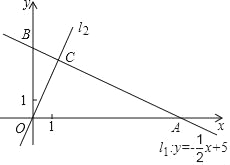
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,点D , E , F分别是边AB , AC , BC上的点,DE∥BC , EF∥AB , 且AD:DB=4:7,那么CF:CB等于( ) 
A.7:11
B.4:8
C.4:7
D.3:7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com