
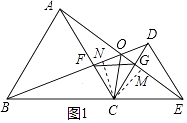
【题目】如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个. 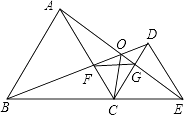
A.5
B.4
C.3
D.2
【答案】B
【解析】解:①∵△ABC和△DCE均是等边三角形, ∴BC=AC,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠BCD=180°﹣60°=∠ACE.
在△BCD和△ACE中, 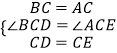 ,
,
∴△BCD≌△ACE(SAS),
∴BD=AE,结论①成立;
②∵△BCD≌△ACE,
∴∠CBF=∠CAG.
∵∠ACB=60°,∠DCE=60°,
∴∠ACG=180°﹣∠ACB﹣∠DCE=60°.
在△BCF和△ACG中, 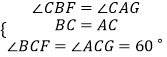 ,
,
∴△BCF≌△ACG(ASA),
∴BF=AG,结论②不成立;
③∵△BCF≌△ACG,
∴CF=CG.
∵∠FCG=60°,
∴△CFG为等边三角形,
∴∠CFG=60°.
∵∠BCF=60,
∴∠BCF=∠CFG,
∴FG∥BE,结论③成立;
④过点C作CM⊥AE于点M,CN⊥BD于点N,如图所示.
∵△BCD≌△ACE,
∴∠CDN=∠CEM.
在△CDN和△CEM中, 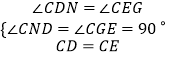 ,
,
∴△CDN≌△CEM(AAS),
∴CM=CN,
∴OC为∠BOE的角平分线,
∴∠BOC=∠EOC,结论④成立;
⑤在AE上寻找点P,连接CP使得CP=CO,如图2所示.
∵△CDN≌△CEM,
∴EM=DN,
∵BD=AE,BF=AG,
∴MG=NF.
在△CMG和△CNF中, 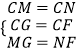 ,
,
∴△CMG≌△CNF(SSS),
∴∠MCG=∠NCF,
∴∠MCN=∠GCF=60°,
∴∠MON=360°﹣∠MCN﹣90°﹣90°=120°.
∵∠BOC=∠EOC,
∴∠BOC=∠EOC= ![]() ∠MON=60°,
∠MON=60°,
∴∠COD=180°﹣∠BOC=120°.
∵CP=CO,∠COP=60°,
∴△COP为等边三角形,
∴∠CPO=60°,OP=OC,
∴∠CPE=180°﹣∠CPO=120°=∠COD.
在△COD和△CPE中, 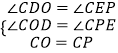 ,
,
∴△COD≌△CPE(AAS),
∴OD=PE.
∴BO=BD﹣OD=AE﹣PE=AO+OP=AO+OC,结论⑤成立.
综上所述:正确的结论有①③④⑤.
故选B.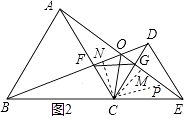
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.


科目:初中数学 来源: 题型:
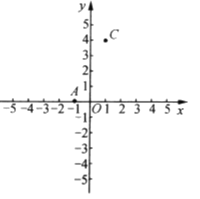
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( ) 
A.2 ![]() π
π
B.![]() π
π
C.2π
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2﹣4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( ) 
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
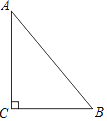
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是⊙O的内接三角形,BC= ![]() .如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=
.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA= ![]() BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 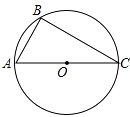
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF.
(1)求证:四边形ACEF是矩形;
(2)求四边形ACEF的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com