
【题目】如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF.
(1)求证:四边形ACEF是矩形;
(2)求四边形ACEF的周长.

【答案】(1)见解析;(2)2+2![]()
【解析】
(1)由DE=AD,DF=CD,根据对角线互相平分的四边形是平行四边形可得四边形ACEF是平行四边形,继而由四边形ABCD为菱形,可以推导得到AE=CF,问题即可得到证明;
(2) 由三角形ADC为等边三角形,得到AC=AB=1,利用矩形的性质可得∠ACE=90,继而可得∠AEC=30,根据30度角的直角三角形的性质可得AE=2AC=2,继而根据勾股定理求得CE长,根据矩形的周长公式即可得答案.
(1)∵DE=AD,DF=CD,
∴四边形ACEF是平行四边形,
∵四边形ABCD为菱形,
∴AD=CD,
∴DE=AD=DF=CD ,
∴AE=CF,
∴四边形ACEF是矩形,
(2)∵菱形ABCD,
∴∠ADC=∠B=60,AD=AB=1,
∵AD=CD,
∴△ACD是等边三角形,
∴AC=AD=1,∠CAD=60,
∵矩形ACEF,
∴∠ACE=90,
∴∠AEC=30,
∴AE=2AC=2,CE=![]() ,
,
∴四边形ACEF的周长为:2(AC+CE) =2+2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个. 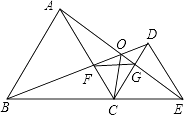
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形EFGH在边长为4的正方形ABCD所在平面上移动,始终保持EF//AB,CK=1.线段KG的中点为M,DH的中点为N,则线段MN的长为 ( ).

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )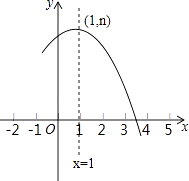
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com