
【题目】如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( ) 
A.2 ![]() π
π
B.![]() π
π
C.2π
D.2 ![]()
【答案】B
【解析】解:如图,连接PA、PC,取AB、BC的中点E、F,连接EF、EM、FM. 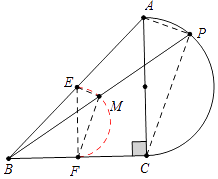
∵AC是直径,
∴∠APC=90°,
∵BE=EA,BM=MP,
∴EM∥PA,同理FM∥PC,
∴∠BME=∠BPA,∠BMF=∠BPC,
∴∠BME+∠BMF=∠BPA+∠BPC=90°,
∴∠EMF=90°,
∴点M的轨迹是 ![]() ,(EF为直径的半圆,图中红线部分)
,(EF为直径的半圆,图中红线部分)
∵BC=AC,∠ACB=90°,AB=8,
∴AC=4 ![]() ,EF=
,EF= ![]() AC=2
AC=2 ![]() ,
,
∴ ![]() 的长=π
的长=π ![]() =
= ![]() π.
π.
故选B.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°).


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,若
中,若![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() 分别在
分别在![]() 和
和![]() 上,且
上,且![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() (如图
(如图![]() ),则可以得到以下两个结论:
),则可以得到以下两个结论:
①![]() ;②
;②![]() .
.
那么在![]() 中,仍然有条件“
中,仍然有条件“![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() ,分别在
,分别在![]() 和
和![]() 上”,请探究以下两个问题:
上”,请探究以下两个问题:
![]() 若
若![]() (如图
(如图![]() ),则
),则![]() 与
与![]() 是否仍相等?若仍相等,请证明;否则请举出反例.
是否仍相等?若仍相等,请证明;否则请举出反例.
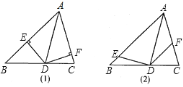
![]() 若
若![]() ,则
,则![]() 是否成立?(只写出结论,不证明)
是否成立?(只写出结论,不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.
(1)集训前小杰射击成绩的众数为 ;
(2)分别计算小杰集训前后射击的平均成绩;
(3)请用一句话评价小杰这次集训的效果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=m是平行于x轴的直线,将抛物线y=﹣ ![]() x2﹣4x在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图象,若新的函数图象刚好与直线y=﹣x有3个交点,则满足条件的m的值为 .
x2﹣4x在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图象,若新的函数图象刚好与直线y=﹣x有3个交点,则满足条件的m的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个. 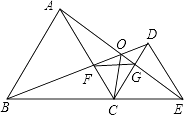
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com