
【题目】直线y=m是平行于x轴的直线,将抛物线y=﹣ ![]() x2﹣4x在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图象,若新的函数图象刚好与直线y=﹣x有3个交点,则满足条件的m的值为 .
x2﹣4x在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图象,若新的函数图象刚好与直线y=﹣x有3个交点,则满足条件的m的值为 .
【答案】0或﹣ ![]()
【解析】解:根据题意 ①当m=0时,新的函数B的图象刚好与直线y=x有3个不动点;
②当m<0时,且翻折后的部分与直线y=x有一个交点,
∵y=﹣ ![]() x2﹣4x=﹣
x2﹣4x=﹣ ![]() (x+4)2+8,
(x+4)2+8,
∴顶点为(﹣4,8),
∴在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分的顶点为(﹣4,﹣8﹣2m),
∴翻折后的部分的解析式为y= ![]() (x+4)2﹣8﹣2m,
(x+4)2﹣8﹣2m,
∵翻折后的部分与直线y=x有一个交点,
∴方程 ![]() (x+4)2﹣8﹣2m=x有两个相等的根,
(x+4)2﹣8﹣2m=x有两个相等的根,
整理方程得x2+6x﹣4m=0.
∴△=36+16m=0,
解得m=﹣ ![]() ,
,
综上,满足条件的m的值为0或﹣ ![]() .
.
所以答案是:0或﹣ ![]() .
.
【考点精析】本题主要考查了二次函数图象的平移的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC=2cm,线段BC上一动点P从C点开始运动,到B点停止,以AP为边在AC的右侧作等边△APQ,则Q点运动的路径为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
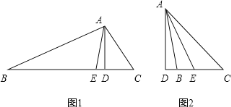
【题目】如图![]() ,在
,在![]() 中,
中,![]() 为
为![]() 边上的高,
边上的高,![]() 为
为![]() 的平分线,已知
的平分线,已知![]() ,
,![]()
![]() 求
求![]() 的度数;
的度数;
![]() 你发现
你发现![]() 与
与![]() 、
、![]() 之间有何关系?
之间有何关系?
![]() 若将“题中的条件
若将“题中的条件![]() ”改为“
”改为“![]() ”如图
”如图![]() ,其它条件不变,则
,其它条件不变,则![]() 与
与![]() 、
、![]() 之间又有何关系?请说明理由.
之间又有何关系?请说明理由.
![]() 若将“题目中的条件
若将“题目中的条件![]() ,
,![]() ”改为“
”改为“![]() ,
,![]() ”,其它条件不变,求
”,其它条件不变,求![]() 、
、![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( ) 
A.2 ![]() π
π
B.![]() π
π
C.2π
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米. 
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com