练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在△ABC中，∠C=90°,D、E分别为AB、AC边上的两点，且AD·AB=AE·AC,求证：DE⊥AB.
    证明：∵AD·AB=AE·AC  ∴   ∵∠A=∠A                         ∴△ADE∽△ACB ∴∠ADE=∠C    ∵∠C=90° ∴∠ADE=90° ∴DE⊥AB
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

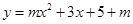    在平面直角坐标系xOy中，抛物线与x轴交于A、B两点（点A
    在点B的左侧），与y轴交于点C（0 , 4），D为OC的中点.
    小题1:（1）求m的值；
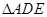    小题2:（2）抛物线的对称轴与x轴交于点E，在直线AD上是否存在点F，使得以点A、B、F为顶点的三角形与 相似？若存在，请求出点F的坐标，若不存在，请说明理由； 
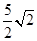    小题3:（3）在抛物线的对称轴上是否存在点G，使△GBC中BC边上的高为？若存在，求出点G的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知：如图，DE∥BC交BA的延长线于D，交CA的延长线于E，AD=4，DB=12，DE=3.
     
    求BC的长.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，AB•AC=AD•AE，且∠1=∠2，求证：△ABC∽△AED．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （本题6分）已知：如图，△ABC是等边三角形，D是AB边上的点，将DB绕点D顺时针旋转60°得到线段DE，延长ED交AC于点F，连结DC、AE．

    小题1:（1）求证：△ADE≌△DFC；
    小题2:（2）过点E作EH∥DC交DB于点G，交BC于点H，连结AH．求∠AHE的度数；
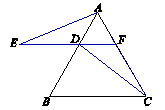
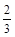    小题3:（3）若BG=，CH=2，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    若两个相似三角形的相似比是1:4,则它们的周长是(      )
    A．1:2B．1:4C．1:16D．1:5

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

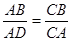    如图，在△ABC中，点D在BC上，在下列四个条件：①∠BAD=∠C；②∠ADC+∠BAC=180°； ③BA2=BD·BC；④中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【   】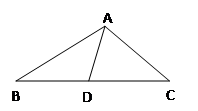 
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在矩形ABCD中，AB =6，AD =11．直角尺的直角顶点P在AD上滑动时（点P与A,D不重合），一直角边始终经过点C，另一直角边与AB交于点E．
    （1）△CDP与△PAE相似吗？如果相似，请写出证明过程；
    （2）当∠PCD =30°时，求AE的长；
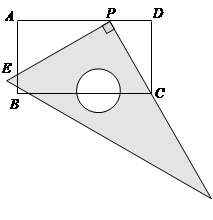    （3）是否存在这样的点P，使△CDP的周长等于△PAE周长的2倍？若存在，求DP的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

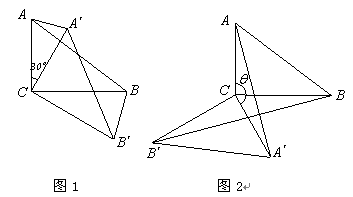
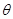    如图1，在△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕顶点C顺时针旋转30°，得到△A′B′C．联结A′A、B′B，设△ACA′和△BCB′的面积分别为S△ACA′ 和S△BCB′．

    小题1:（1）直接写出S△ACA′ ︰S△BCB′ 的值                  ；
    小题2:（2）如图2，当旋转角为（0°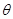＜＜180°）时，S△ACA′ 与S△BCB′ 的比值是否发生变化，若不变请证明；若改变，写出变化后的比值（可用含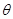的代数式表示）．

    查看答案和解析>>

    同步练习册答案