【题目】若关于x的一元二次方程(p-1)x2-x+p2-1=0的一个根为0，则p的值为_________.
科目：初中数学 来源： 题型：
【题目】已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣(t﹣4)2+20．若此礼炮在升空到最高处时引爆，则引爆需要的时间为( )
A.3sB.4sC.5sD.6s
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】大家知道
，它在数轴上的意义是表示
的点与原点（即表示
的点）之间的距离，又如式子
，它在数轴上的意义是表示
的点与表示
的点之间的距离．
（
）在数轴上的意义是表示
的点与表示
的点之间的距离是__________．
（
）反过来，式子
在数轴上的意义是__________．
（
）试用数轴探究：当
时， 
的值为__________．
（
）进一步探究： 
的最小值为__________．
（
）最后发现：当
的值最小时， 
的值为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若存在3个互不相同的有理数a，b，c，使得|1﹣a|+|1﹣3a|+|1﹣4a|=|1﹣b|+|1﹣3b|+|1﹣4b|=|1﹣c|+|1﹣3c|+|1﹣4c|=t，则t=
A. 
B. 
C. 1 D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
小丁在研究数学问题时遇到一个定义：对于排好顺序的三个数： 
，称为数列
.计算
， 
， 
将这三个数的最小值称为数列
的价值．例如，对于数列2，﹣1，3，因为
， 
， 
，所以数列2，﹣1，3的价值为
．
小丁进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的价值．如数列﹣1，2，3的价值为
；数列3，﹣1，2的价值为1；…．经过研究，小丁发现，对于“2，﹣1，3”这三个数，按照不同的排列顺序得到的不同数列中，价值的最小值为
．根据以上材料，回答下列问题：
（1）数列﹣4，﹣3，2的价值为 ；
（2）将“﹣4，﹣3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的价值的最小值为 ，取得价值最小值的数列为 （写出一个即可）；
（3）将2，﹣9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的价值的最小值为1，则a的值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（8分）完成下面的解题过程：
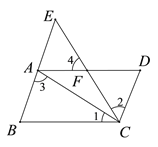
如图，AD∥BC，点F是AD上一点，CF与BA的延长线相交于点E，且∠1=∠2，∠3=∠4．CD与BE平行吗？为什么？
解：CD∥BE，理由如下：
∵AD∥BC（已知），∴∠4= ① （ ② ）
∵∠3=∠4（已知），∴∠3= ③ （ ④ ）
∵∠1=∠2（已知），
∴∠1+∠ACE=∠2+∠ACE （ ⑤ ）
即∠BCE= ⑥
∴∠3= ⑦
∴CD∥BE（ ⑧ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场试销一种成本为每件120元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量
（件）是销售单价
（元）的函数，并且满足如下对应值表：
销售单价 | 130 | 140 | 145 |
销售量 | 110 | 100 | 95 |
（1）求
与
的函数表达式；
（2）若该商场获得利润为
元，试写出利润
与销售单价
之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
（3）若该商场获得利润不低于 2000元，试确定销售单价
的范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
