
 如图,边长为6的正方形ABCD中,E是AB边上的一点,且AE=2BE,已知F是CE的中点,将△CDF沿着DF翻折至△GDF,连接BG,则S四边形BFDG=$\frac{228}{17}$.
如图,边长为6的正方形ABCD中,E是AB边上的一点,且AE=2BE,已知F是CE的中点,将△CDF沿着DF翻折至△GDF,连接BG,则S四边形BFDG=$\frac{228}{17}$. 分析 如图,连接CG交DF于M、作FN⊥BC于N,FP⊥DC于P,FH⊥BG于H.则四边形FNCP是矩形,在△DFC中,求出高CM,FP,由△CMD∽△BHF,得$\frac{CD}{BF}$=$\frac{CM}{BH}$=$\frac{DM}{FH}$,可以求出FH,BH,BG,再根据S四边形BFDG=S△BFG+S△DGF计算即可解决问题.
解答 解:如图,连接CG交DF于M、作FN⊥BC于N,FP⊥DC于P,FH⊥BG于H.则四边形FNCP是矩形,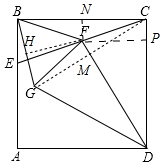
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=6,∠ABC=∠BCD=90°,
∵AE=2BE,
∴AE=4,BE=2,
∵FN∥AB,EF=FC,
∴NB=CN=FP=3,FN=$\frac{1}{2}$EB=PC=1,
∴PD=5,DF=$\sqrt{F{P}^{2}+P{D}^{2}}$=$\sqrt{34}$,CF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵DG=DC,FG=FC,
∴DF⊥CG,
∵$\frac{1}{2}$CD•FP=$\frac{1}{2}$•DF•CM,
∴CM=$\frac{9\sqrt{34}}{17}$,DM=$\sqrt{D{C}^{2}-C{M}^{2}}$=$\frac{15\sqrt{34}}{17}$,
在Rt△BCE中,EC=$\sqrt{B{E}^{2}+B{C}^{2}}$=2$\sqrt{10}$,
∵EF=FC,
∴BF=EF=FC=FG=$\sqrt{10}$,
∴∠FBC=∠FCB,∠FGC=∠FCG,
∵∠BFE=∠FBC+∠FCB,∠EFC=∠FGC+∠FCG,
∴∠BFG=2∠BCG,
∵BF=FG,FH⊥BG,
∴∠BFH=∠GFH=∠BCG,BH=HG,
∵∠HBF+∠BFH=90°,∠BCG+∠DCG=90°,
∴∠DCM=∠FBH,∵∠CMD=∠FHB,
∴△CMD∽△BHF,
∴$\frac{CD}{BF}$=$\frac{CM}{BH}$=$\frac{DM}{FH}$,
∴$\frac{6}{\sqrt{10}}$=$\frac{\frac{9\sqrt{34}}{17}}{BH}$=$\frac{\frac{15\sqrt{34}}{17}}{FH}$,
∴BH=$\frac{3\sqrt{340}}{34}$,FH=$\frac{5\sqrt{170}}{34}$$\frac{5\sqrt{340}}{34}$,
∴BG=2BH=$\frac{3\sqrt{340}}{17}$,
∴S四边形BFDG=S△BFG+S△DGF=$\frac{1}{2}$•$\frac{3\sqrt{340}}{17}$•$\frac{5\sqrt{340}}{34}$•+$\frac{1}{2}$×6×3=$\frac{228}{17}$.
故答案为$\frac{228}{17}$.
点评 本题考查翻折变换、正方形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会利用面积法求高,属于中考


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是⊙O的内接四边形,点E是DC延长线上一点,且CB=CE,连接BE,若∠E=40°,则∠A的度数为( )
如图,四边形ABCD是⊙O的内接四边形,点E是DC延长线上一点,且CB=CE,连接BE,若∠E=40°,则∠A的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 3和3 2 | B. | -2 3和(-2)3 | C. | -3 2和(-3)2 | D. | (-3×2)2和-3 2×2 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com