
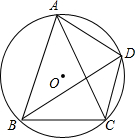
 已知点A、B、C、D四点在O上;
已知点A、B、C、D四点在O上;分析 (1)由∠ABC=∠ADB,根据圆周角与弧的关系,可证得$\widehat{AC}$=$\widehat{AB}$,又由弧与弦的关系,即可证得结论;
(2)由圆周角定理可证得:∠CAD=∠CBD,∠ACD=∠ABD,又由∠CAD=∠ACD,即可证得结论.
解答 证明:(1)∵∠ABC=∠ADB,
∴$\widehat{AC}$=$\widehat{AB}$,
∴AB=AC;
(2)∵∠CAD=∠CBD,∠ACD=∠ABD,
又∵∠CAD=∠ACD,
∴∠ABD=∠CBD,
∴BD平分∠ABC.
点评 此题考查了圆周角定理以及弧与弦的关系.注意在同圆或等圆中,同弧或等弧所对的圆周角相等.


科目:初中数学 来源: 题型:选择题
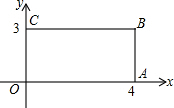 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )| A. | 5 | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明从如图中的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①b<0;②c=0;③函数的最小值为-3;④4a+2b-5c<0;⑤当x1<x2<2时,y1>y2.你认为其中正确的有①②③④⑤.
小明从如图中的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①b<0;②c=0;③函数的最小值为-3;④4a+2b-5c<0;⑤当x1<x2<2时,y1>y2.你认为其中正确的有①②③④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
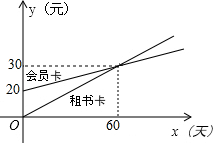 某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com