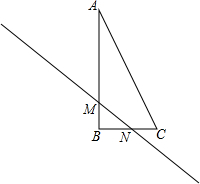Question

13．如图，在直角三角形ABC中，∠B=90°，点M，N分别在边AB，BC上，且BM=BN，
（1）画出直角三角形ABC关于直线MN对称的三角形A′B′C′；
（2）如果AB=a，BC=b，BM=x，用含a，b，x的代数式分别表示三角形AMA′的面积S₁和四边形ACA′C′的面积S，并化简．

Answer 1

分析 （1）作出点A、B、C关于直线MN的对称点A′、B′、C′，然后顺次连接即可；
（2）先判断出△AMA′是等腰直角三角形，然后根据等腰直角三角形的面积等于直角边的平方的一半列式进行计算即可得解；再根据四边形AA′C′C的面积S=△AMA′的面积+△CNC′的面积+△ABC的面积+△A′B′C′的面积-正方形BNB′M的面积，然后列式进行计算即可得解．

解答 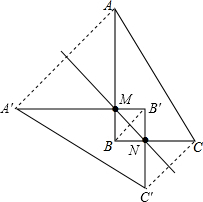解：（1）△A′B′C′如图所示；

（2）∵∠B=90°，BM=BN，
∴△BMN是等腰直角三角形，
∴△AMA′是等腰直角三角形，
∴△AMA'的面积S₁=$\frac{1}{2}$（a-x）²=$\frac{1}{2}$a²-ax+$\frac{1}{2}$x²；
四边形AA′C′C的面积S=△AMA′的面积+△CNC′的面积+△ABC的面积+△A′B′C′的面积-正方形BNB′M的面积
=$\frac{1}{2}$（a-x）²+$\frac{1}{2}$（b-x）²+$\frac{1}{2}$ab+$\frac{1}{2}$ab-x²
=$\frac{1}{2}$a²+$\frac{1}{2}$b²-ax-bx+ab．

点评 本题考查了利用轴对称变换作图，等腰直角三角形的判定与性质，三角形的面积，把四边形的面积分成四个三角形的面积和减去正方形的面积是解题的关键，也是本题的难点．