
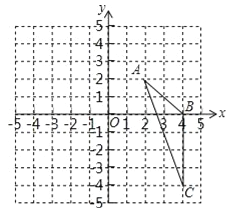
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
试题分析:(1)将A、B、C三点分别向左平移6个单位即可得到的△A1B1C1;
(2)连接OA、OC,分别取OA、OB、OC的中点即可画出△A2B2C2,求出直线AC与OB的交点,求出∠ACB的正弦值即可解决问题.
试题解析:(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1,如图1所示,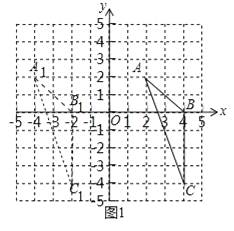
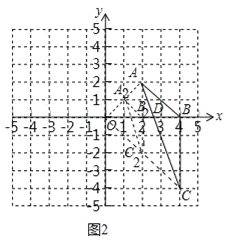
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,如图2所示,∵A(2,2),C(4,﹣4),B(4,0),∴直线AC解析式为y=﹣3x+8,与x轴交于点D(
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,如图2所示,∵A(2,2),C(4,﹣4),B(4,0),∴直线AC解析式为y=﹣3x+8,与x轴交于点D(![]() ,0),∵∠CBD=90°,∴CD=
,0),∵∠CBD=90°,∴CD=![]() =
=![]() ,∴sin∠DCB=
,∴sin∠DCB=![]() =
=![]() =
=![]() .
.
∵∠A2C2B2=∠ACB,∴sin∠A2C2B2=sin∠DCB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N. 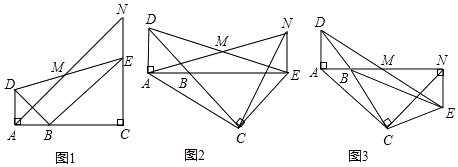
(1)当A、B、C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A、B、E三点在同一直线上(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江西省)设抛物线的解析式为![]() ,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点
,过点B1 (1,0 )作x轴的垂线,交抛物线于点A1(1,2 );过点B2 (1,0 )作x轴的垂线,交抛物线于点A2 ,… ;过点![]() (
(![]() ,0 ) (n为正整数 )作x轴的垂线,交抛物线于点
,0 ) (n为正整数 )作x轴的垂线,交抛物线于点![]() ,连接
,连接![]() ,得直角三角形
,得直角三角形![]() .
.
(1)求a的值;
(2)直接写出线段![]() ,
,![]() 的长(用含n的式子表示);
的长(用含n的式子表示);
(3)在系列Rt△![]() 中,探究下列问题:
中,探究下列问题:
①当n为何值时,Rt△![]() 是等腰直角三角形?
是等腰直角三角形?
②设1≤k<m≤n (k,m均为正整数),问是否存在Rt△![]() 与Rt△
与Rt△![]() 相似?若存在,求出其相似比;若不存在,说明理由.
相似?若存在,求出其相似比;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOC=∠BOD=α(0°<α<180°)
(1)如图1,若α=90°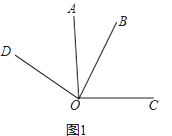
①写出图中一组相等的角(除直角外) , 理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是;当α=°,∠COD和∠AOB互余.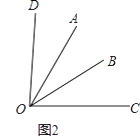
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个商贩同时卖出两件上衣,售价都是140元.按成本计算,其中一件盈利75%,另一件亏损30%,在这次交易中,该商贩( )
A.不赔不赚
B.赚10元
C.赔10元
D.赔20元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行
(2)过一点有且只有一条直线与已知直线垂直
(3)在同一平面内,两条直线的位置关系只有相交、平行两种
(4)不相交的两条直线叫做平行线
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com