
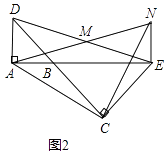
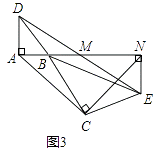
����Ŀ����ͼ����֪��BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬��MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N�� 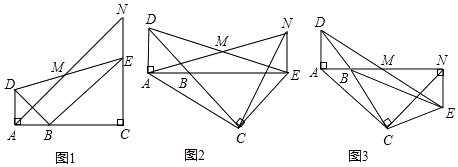
��1����A��B��C������ͬһֱ����ʱ����ͼ1������֤��MΪAN���е㣻
��2����ͼ1�С�BCE�Ƶ�B��ת����A��B��E������ͬһֱ���ϣ���ͼ2������֤����CANΪ����ֱ�������Σ�
��3����ͼ1�С�BCE�Ƶ�B��ת��ͼ3��λ��ʱ����2���еĽ����Ƿ���Ȼ����������������֤��֮��������������˵�����ɣ�
���𰸡�
��1���⣺֤������ͼ1����EN��AD��
���MAD=��MNE����ADM=��NEM��
�ߵ�MΪDE���е㣬
��DM=EM��
�ڡ�ADM�͡�NEM�У�
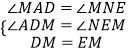 ��
��
���ADM�ա�NEM��AAS����
��AM=MN��
��MΪAN���е�
��2���⣺֤������ͼ2���ߡ�BAD�͡�BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45�㣬
��AD��NE��
���DAE+��NEA=180�㣬
�ߡ�DAE=90�㣬
���NEA=90�㣬
���NEC=135�㣬
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135�㣬
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
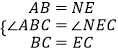 ��
��
���ABC�ա�NEC��SAS����
��AC=NC����ACB=��NCE��
�ߡ�BCE=90�㣬
���ACN=��BCE=90�㣬
���ACNΪ����ֱ�������Σ�
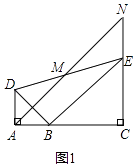
��3���⣺��ACN��Ϊ����ֱ�������Σ�
֤������ͼ3��A��B��N������ͬһ��ֱ���ϣ�
��AD��EN����DAB=90�㣬
���ENA=��DAN=90�㣬
�ߡ�BCE=90�㣬
���CBN+��CEN=360�㩁90�㩁90��=180�㣬
��A��B��N������ͬһ��ֱ���ϣ�
���ABC+��CBN=180�㣬
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
�ڡ�ABC�͡�NEC�У�
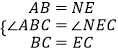 ��
��
���ABC�ա�NEC��SAS����
��AC=NC����ACB=��NCE��
���ACN=��BCE=90�㣬
���ACNΪ����ֱ�������Σ�
����������1����EN��AD�͵�MΪDE���е㣬����֤�á�ADM�ա�NEM���Ӷ�֤��MΪAN���е㣻��2��������֪��������֤AB=DA=NE����ABC=��NEC=135�㣬�Ӷ��ɵá�ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90�㣬�ɵá�ACNΪ����ֱ�������Σ���3��������֪�������á�ADM�ա�NEM�������ı���BCEF�ڽǺ�Ϊ360�㣬�ɵá�ABC=��FEC���Ӷ�����֤�á�ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90�㣬���ɵó���ACNΪ����ֱ�������Σ�
�����㾫�����������⣬������Ҫ�˽����ֱ��������(����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45��)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
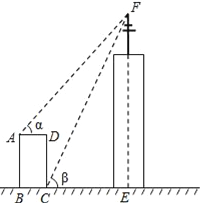
����Ŀ����ͼ��ij��¥������һ�źŷ�������С���ھ��ν�����ABCD��A��C���㴦�������F�����Ƿֱ�Ϊ���ͦ£�AD=18m��CD=78m��
��1���æ��ͦµ����Ǻ�����ʾCE��
��2������=30�㡢��=60��ʱ����EF�������ȷ��1m����
���ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�������Գ�ͼ�Σ��������ĶԳ�ͼ�ε��ǣ�������
A.��������B.ƽ���ı���C.��������D.Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ� ��ͼ1����Rt��ABC�У���C=90�㣬DΪ��AC��һ�㣬DA=DB��EΪBD�ӳ�����һ�㣬��AEB=120�㣬����AC��BE��AE��������ϵ����֤����
С����˼·�ǣ����ݵ�����ADB����Գ��ԣ�������ͼ������AB�ߵĴ�ֱƽ���߷��ۣ��õ���C�ĶԳƵ�F����ͼ2������A��AF��BE����BE���ӳ�����F���벹����ɴ����⣻
�ο�С��˼������ķ���������������⣺
��ͼ3��������ABC�У�AB=AC��D��F��ֱ��BC�ϣ�DE=BF������AD������E��EG��AC��FH���ӳ����ڵ�G����DFG+��D=��BAC��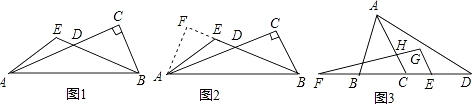
��1��̽����BAD���CHG��������ϵ��
��2������ͼ���ҳ�һ�����߶�AD��ȵ��߶Σ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����ͬѧ�ļ���ѧУ�ľ����Ϊ3000�ף���ͬѧ�Ȳ���600�ף�Ȼ��˹�����ȥѧУ����ͬѧ�����г�ȥѧУ����֪�ײ����ٶ����������г��ٶȵ� ![]() �����������ٶ����������г��ٶȵ�2����������ͬѧͬʱ�Ӽҷ�ȥѧУ�������ͬѧ����ͬѧ�絽2���ӣ�
�����������ٶ����������г��ٶȵ�2����������ͬѧͬʱ�Ӽҷ�ȥѧУ�������ͬѧ����ͬѧ�絽2���ӣ�
��1�����������г����ٶȣ�
��2��������ѧУʱ����ͬѧ��ѧУ���ж�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
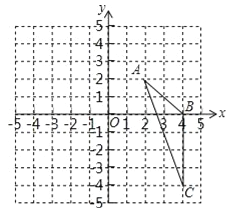
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC�������������ֱ���A��2��2����B��4��0����C��4����4��
��1���뻭����ABC����ƽ��6����λ���Ⱥ�õ��ġ�A1B1C1��
��2���Ե�OΪλ�����ģ�����ABC��СΪԭ����![]() ���õ���A2B2C2������y���Ҳ����A2B2C2���������A2C2B2������ֵ��
���õ���A2B2C2������y���Ҳ����A2B2C2���������A2C2B2������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��AB�ǰ�ԲO��ֱ������AD��BC�ཻ�ڵ�P����ô ![]() ���ڡ�BPD�ģ� ��
���ڡ�BPD�ģ� �� 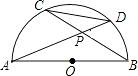
A.����
B.����
C.����
D.���϶�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com