
【题目】阅读下列材料: 如图1,在Rt△ABC中,∠C=90°,D为边AC上一点,DA=DB,E为BD延长线上一点,∠AEB=120°,猜想AC、BE、AE的数量关系,并证明.
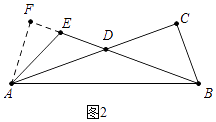
小明的思路是:根据等腰△ADB的轴对称性,将整个图形沿着AB边的垂直平分线翻折,得到点C的对称点F,如图2,过点A作AF⊥BE,交BE的延长线于F,请补充完成此问题;
参考小明思考问题的方法,解答下列问题:
如图3,等腰△ABC中,AB=AC,D、F在直线BC上,DE=BF,连接AD,过点E作EG∥AC交FH的延长线于点G,∠DFG+∠D=∠BAC.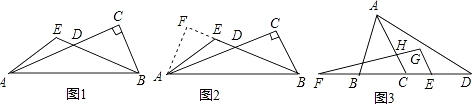
(1)探究∠BAD与∠CHG的数量关系;
(2)请在图中找出一条和线段AD相等的线段,并证明.
【答案】
(1)解:阅读材料,如图2中,结论:AC=BE+ ![]() AE.理由如下,
AE.理由如下,
∵DA=DB,
∴∠DAB=∠DBA,
∵AF⊥BF,
∴∠F=∠C=90°,
在△ABF和△BAC中,
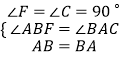 ,
,
∴△ABF≌△BAC,
∴AC=BF,
∵∠AEB=120°=∠F+∠FAE,
∴∠FAE=30°,∴EF= ![]() AE,
AE,
∴AC=BF=BE+EF=BE+ ![]() AE,
AE,
∴AC=BE+ ![]() AE.
AE.
问题:(1)如图3中,
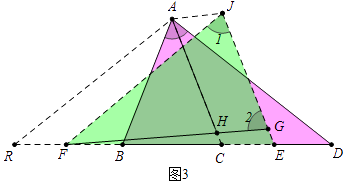
∵∠ACD=∠D+∠CAD,∠D+∠CFG=∠BAC,
∴∠CHG=∠CFH+∠FCH=∠CFH+∠D+∠CAD=∠BAC+∠CAD=∠BAD,
∴∠CHG=∠BAD.
(2)解:结论:AD=FG.理由如下,
如图3中,延长BF到R,使得BR=CD,连接AR,作AJ∥CD交EG的延长线于J,连接FJ.
∵AJ∥CE,AC∥JE,
∴四边形ACEJ,四边形ACGK是平行四边形,
∴AJ=CE,AC=JE,
∵AB=CA,
∴JE=AB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABR=∠ACD,
在△ABR和△ACD中,
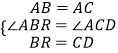 ,
,
∴△ABR≌△ACD,
∴AR=AD,
∵BR=CD,BF=ED,
∴FR=CE=AJ,EF=BD,∵AJ∥RF,
∴四边形ARFJ是平行四边形,
∴JF=AR=AD,
在△ABD和△JEF中,
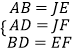 ,
,
∴△ABD≌△JEF,
∴∠1=∠BAD,
∵∠BAD=∠CHG=∠2,
∴∠1=∠2,
∴FG=FJ,
∴AD=FG.
【解析】阅读材料:如图2中,结论:AC=BE+ ![]() AE.理由如下,只要证明△ABF≌△BAC,推出AC=BF,再证明EF=
AE.理由如下,只要证明△ABF≌△BAC,推出AC=BF,再证明EF= ![]() AE,可得AC=BF=BE+EF=BE+
AE,可得AC=BF=BE+EF=BE+ ![]() AE. 问题:(1)由∠ACD=∠D+∠CAD,∠D+∠CFG=∠BAC,推出∠CHG=∠CFH+∠FCH=∠CFH+∠D+∠CAD=∠BAC+∠CAD=∠BAD,可得∠CHG=∠BAD.(2)结论:AD=FG.如图3中,延长BF到R,使得BR=CD,连接AR,作AJ∥CD交EG的延长线于J,连接FJ.首先证明四边形ACEJ,四边形AJFR是平行四边形,再证明△ABD≌△JEF,想办法证明∠1=∠2,即可解决问题.
AE. 问题:(1)由∠ACD=∠D+∠CAD,∠D+∠CFG=∠BAC,推出∠CHG=∠CFH+∠FCH=∠CFH+∠D+∠CAD=∠BAC+∠CAD=∠BAD,可得∠CHG=∠BAD.(2)结论:AD=FG.如图3中,延长BF到R,使得BR=CD,连接AR,作AJ∥CD交EG的延长线于J,连接FJ.首先证明四边形ACEJ,四边形AJFR是平行四边形,再证明△ABD≌△JEF,想办法证明∠1=∠2,即可解决问题.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).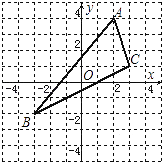
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“配方法”解一元二次方程x2﹣16x+24=0,下列变形结果,正确的是( )
A.(x﹣4)2=8B.(x﹣4)2=40C.(x﹣8)2=8D.(x﹣8)2=40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③ ![]() (∠α+∠β);④
(∠α+∠β);④ ![]() (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N. 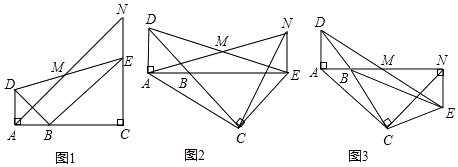
(1)当A、B、C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A、B、E三点在同一直线上(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行
(2)过一点有且只有一条直线与已知直线垂直
(3)在同一平面内,两条直线的位置关系只有相交、平行两种
(4)不相交的两条直线叫做平行线
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com