练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ABC中，A点坐标为（2，4），B点坐标为（﹣3，﹣2），C点坐标为（3，1）．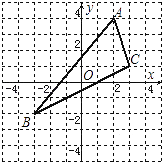

    （1）在图中画出△ABC关于y轴对称的△A′B′C′（不写画法），并写出点A′，B′，C′的坐标．
    （2）求△ABC的面积．

    【答案】
    （1）

    解：如图，A′（﹣2，4），B′（3，﹣2），C′（﹣3，1）


    （2）

    解：S△ABC=6×6﹣ ×5×6﹣ ×6×3﹣ ×1×3，

    =36﹣15﹣9﹣1 ，

    =10


    【解析】（1）根据网格结构找出点A′、B′、C′的位置，然后顺次连接即可；（2）利用三角形所在的矩形的面积减去四周三个小直角三角形的面积，然后列式计算即可得解．
    【考点精析】本题主要考查了作轴对称图形的相关知识点，需要掌握画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知E、F、G、H分别为菱形ABCD四边的中点，AB=6cm，∠ABC=60°，则四边形EFGH的面积为 cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

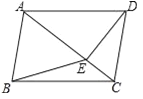
    【题目】如图，在四边形ABCD中，AB∥CD，∠ABC=∠ADC，DE垂直于对角线AC，垂足是E，连接BE．

    （1）求证：四边形ABCD是平行四边形；

    （2）若点E是AC的中点，判断BE与AC的位置关系，并说明理由；

    （3）若△ABE是等边三角形，AD=，求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正方形ABCD中，BC=3，点E、F分别是CB、CD延长线上的点，DF=BE，连接AE、AF，过点A作AH⊥ED于H点．

    （1）求证：△ADF≌△ABE；

    （2）若BE=1，求tan∠AED的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对非负实数x“四舍五入”到个位的值记为[x]．即当n为非负整数时，若n﹣ ≤x＜n+ ，则[x]=n．如：[3.4]=3，[3.5]=4，…根据以上材料，解决下列问题：
    （1）填空：
    ①若[x]=3，则x应满足的条件：；
    ②若[3x+1]=3，则x应满足的条件：；
    （2）求满足[x]= x﹣1的所有非负实数x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动．对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．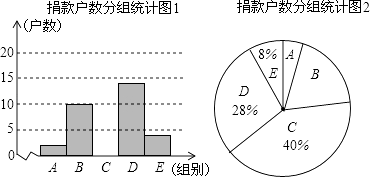

    捐款户数分组统计表

    组别

    捐款额（x）元

    户数

    A

    1≤x＜50

    a

    B

    50≤x＜100

    10

    C

    100≤x＜150

    D

    150≤x＜200

    E

    x≥200

    请结合以上信息解答下列问题．
    （1）a= ， 本次调查样本的容量是；
    （2）补全“捐款户数分组统计表和捐款户数分组统计图1”；
    （3）若该社区有1500户住户，请根据以上信息，估计全社区捐款不少于150元的户数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

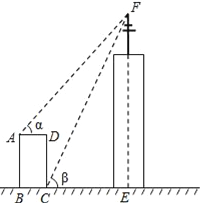
    【题目】如图，某高楼顶部有一信号发射塔，小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β，AD=18m，CD=78m．

    （1）用α和β的三角函数表示CE；

    （2）当α=30°、β=60°时，求EF（结果精确到1m）．

    （参考数据：≈1.414，≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为提高饮水质量，越来越多的居民选购家用净水器．一商场抓住商机，从厂家购进了A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元．
    （1）求A、B两种型号家用净水器各购进了多少台；
    （2）为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元．（注：毛利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料： 如图1，在Rt△ABC中，∠C=90°，D为边AC上一点，DA=DB，E为BD延长线上一点，∠AEB=120°，猜想AC、BE、AE的数量关系，并证明．
    小明的思路是：根据等腰△ADB的轴对称性，将整个图形沿着AB边的垂直平分线翻折，得到点C的对称点F，如图2，过点A作AF⊥BE，交BE的延长线于F，请补充完成此问题；
    参考小明思考问题的方法，解答下列问题：
    如图3，等腰△ABC中，AB=AC，D、F在直线BC上，DE=BF，连接AD，过点E作EG∥AC交FH的延长线于点G，∠DFG+∠D=∠BAC．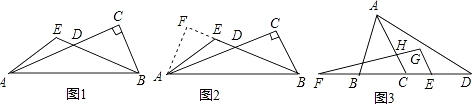

    （1）探究∠BAD与∠CHG的数量关系；
    （2）请在图中找出一条和线段AD相等的线段，并证明．

    查看答案和解析>>

    同步练习册答案