
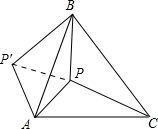
 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB的度数是( )
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB的度数是( )| A. | 120° | B. | 135° | C. | 150° | D. | 105° |
分析 由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,可求得PP′,由△APP′为等边三角形,得∠APP′=60°,在△PP′B中,已知三边,用根据勾股定理逆定理证出直角三角形,得出∠P′PB=90°,可求∠APB的度数.
解答 解:连接PP′,由题意可知AP′=AP=6,
∵旋转角的度数为60°,
∴ ∠PAP′=60°.
∠PAP′=60°.
∴△APP′为等边三角形,
∴PP′=AP=AP′=6;
∵BP′=PC=10,BP=8,PP′=6,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°
∴∠APB=∠BPP′+∠APP′=90°+60°=150°.
故选:C.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质以及勾股定理的逆定理.


科目:初中数学 来源: 题型:填空题
| y(单位:度) | 100 | 200 | 400 | 500 | … |
| x(单位:米) | 1.00 | 0.50 | 0.25 | 0.20 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
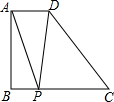 如图,已知梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P为BC边上一个动点,连接PA、PD,则△PAD周长的最小值是2$\sqrt{17}$+2.
如图,已知梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P为BC边上一个动点,连接PA、PD,则△PAD周长的最小值是2$\sqrt{17}$+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
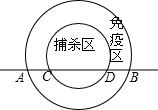 高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com