练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：A+2B=，B=.

    （1）求A；

    （2）若计算A的值.

    【答案】(1)-a2+5ab+14；(2)3.

    【解析】

    (1)根据题意可得A=7a2-7ab-2B，由此可得出A的表达式．

    (2)根据非负性可得出a和b的值，代入可得出A的值．

    解：(1)∵A+2B=7a2-7ab，

    ∴A=7a2-7ab-2B，

    ∵B=4a2-6ab-7，

    ∴A=7a2-7ab-2(4a2-6ab-7)

    =7a2-7ab-8a2+12ab+14

    =-a2+5ab+14；

    (2)∵|a+1|+(b-2)2=0，

    ∴a=-1，b=2，

    ∴A=-a2+5ab+14

    =-(-1)2+5×(-1)×2+14

    =-1-10+14

    =3.

    故答案为：(1)-a2+5ab+14；(2)3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

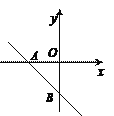
    【题目】直线y＝－x－2交x轴于点A，交y轴于点B，一抛物线的顶点为A，且经过点B．

    （1）求该抛物线的解析式；

    （2）若点C（m，－4.5）在抛物线上，求m的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近几年兴义市加大中职教育投入力度，取得了良好的社会效果。某校随机调查了九年级a名学生升学意向，并根据调查结果绘制如图的两幅不完整的统计图。

    请你根据图中信息解答下列问题：

    （1）a= ;

    （2）扇形统计图中，“职高”对应的扇形的圆心角α= ；

    （3）请补全条形统计图；

    （4）若该校九年级有学生900名，估计该校共有多少名毕业生的升学意向是职高。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．

    （1）求证：△COD是等边三角形；

    （2）当a=150°时，试判断△AOD的形状，并说明理由；

    （3）探究：当a为多少度时，△AOD是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

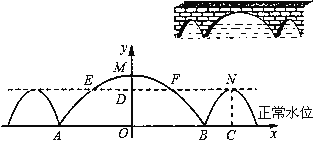
    【题目】如图，三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小都相同．正常水位时，大孔水面宽度AB=20米，顶点M距水面6米（即MO=6米），小孔顶点N距水面4．5米（即NC=4．5米）．当水位上涨刚好淹没小孔时，借助图中的直角坐标系，求此时大孔的水面宽度EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，点E、F分别在边CD、AB上，且DE=BF，∠ECA=∠FCA．

    （1）求证：四边形AFCE是菱形；

    （2）若AB=8，BC=4，求菱形AFCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】早上，甲、乙、丙三人在同一条路上不同起点朝同方向以不同的速度匀速跑:点分时，乙在中间，丙在前，甲在后，且乙与甲、丙的距离相等:点时，甲追上乙；点分时，甲追上丙；当乙追上丙时，若从点分起计时，丙跑的时间为___________分钟.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在ABCD中，对角线AC、BD相交于O，EF过点O，连接AF、CE．

    （1）求证：△BFO≌△DEO；

    （2）若AF⊥BC，试判断四边形AFCE的形状，并加以证明；

    （3）若在（2）的条件下再添加EF平分∠AEC，试判断四边形AFCE的形状，无需说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与反比例函数的图像在第一象限有一个公共点，其横坐标为1，则一次函数的图像可能是（ ）

    A.

    B.

    C.

    D.

    查看答案和解析>>

    同步练习册答案