
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
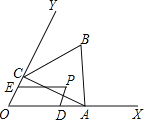
【答案】2≤a+2b≤5.
【解析】
作辅助线,构建30度的直角三角形,先证明四边形EODP是平行四边形,得EP=OD=a,在Rt△HEP中,∠EPH=30°,可得EH的长,计算a+2b=2OH,确认OH最大和最小值的位置,可得结论.
过P作PH⊥OY交于点H,
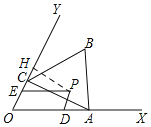
∵PD∥OY,PE∥OX,
∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,
∴EP=OD=a,
Rt△HEP中,∠EPH=30°,
∴EH=![]() EP=
EP=![]() a,
a,
∴a+2b=2(![]() a+b)=2(EH+EO)=2OH,
a+b)=2(EH+EO)=2OH,
当P在AC边上时,H与C重合,此时OH的最小值=OC=![]() OA=1,即a+2b的最小值是2;
OA=1,即a+2b的最小值是2;
当P在点B时,OH的最大值是:1+![]() =
=![]() ,即(a+2b)的最大值是5,
,即(a+2b)的最大值是5,
∴2≤a+2b≤5.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)写出该厂星期一生产工艺品的数量;
(2)本周产量最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
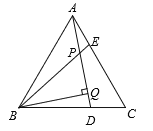
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
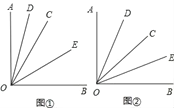
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出∠DOE的度数(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于每个正整数![]() ,设
,设![]() 表示
表示![]() 的末位数字.例如:
的末位数字.例如:![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),…则
的末位数字),…则![]() 的值为( )
的值为( )
A.4040B.4038C.0D.4042
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,且
,且![]() 满足
满足![]() .
.
(1)![]() ,
,![]() ,
,![]() .
.
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与表示 的数的点重合;
与表示 的数的点重合;
(3)点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、点
、点![]() 同时出发),经过几秒,点
同时出发),经过几秒,点![]() 、点
、点![]() 分别到点
分别到点![]() 的距离相等?
的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
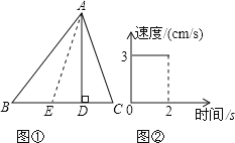
【题目】 如图①所示,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②所示,已知BC=8cm
(1)由图②,E点运动的时间为______s,速度为______cm/s
(2)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;
(3)当E点停止后,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com