
关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2。
(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1且k为整数,求k的值。
(1)k≤0;(2)-1和0.
【解析】
试题分析:(1)∵方程有实数根 ∴Δ=22-4(k+1)≥0解得 k≤0.
(2)根据一元二次方程根与系数的关系,得x1+x2=-2, x1x2=k+1
得-2—(k+1)<-1,解得k>-2,∴-2<k≤0
∵k为整数 ,∴k的值为-1和0.
试题解析:解:∵(1)方程有实数根
∴Δ=22-4k+1)≥0.
解得 k≤0.
k的取值范围是k≤0.
(2)根据一元二 次方程根与系数的关系,得x1+x2=-2, x1x2=k+1
次方程根与系数的关系,得x1+x2=-2, x1x2=k+1
x1+x2-x1x2=-2,+ k+1
由已知,得-2—(k+1)<-1,解得 k>-2
又由(1)k≤0
∴-2<k≤0
∵k为整数
∴k的值为-1和0.
【难度】较易


科目:初中数学 来源: 题型:
某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x件.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=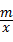 的图象的交点.
的图象的交点.
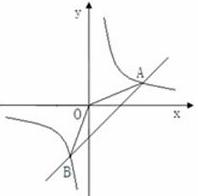
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
| X(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
(1)根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com