如图，已知A （4，a），B （﹣2，﹣4）是一次函数y=kx+b的图象和反比例函数y=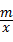
的图象的交点．
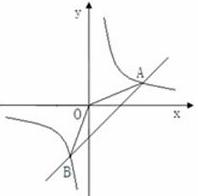
（1）求反比例函数和一次函数的解祈式；
（2）求△A0B的面积．
科目：初中数学 来源： 题型：
如图，直线l上有一点P1（2，1），将点P1先向右平移1个单位，再向上平移2个单位得到像点P2，点P2恰好在直线l上．
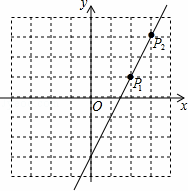
（1）写出点P2的坐标；
（2）求直线l所表示的一次函数的表达式；
（3）若将点P2先向右平移3个单位，再向上平移6个单位得到像点P3．请判断点P3是否在直线l上，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台，记录下某一天各自的销售情况（单位：元）：
甲：l8， 8，10，43， 5，30，10，22， 6，27，25，58，14，18，30，41
乙：22，31，32，42，20，27，48，23，38，43，12，34，18，l0，34，23
小强用如图所示的方法表示甲城市16台自动售货机的销售情况．
（1）请你仿照小强的方法将乙城市16台自动售货机的销售情况表示出来；
（2）用不等号填空：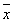
甲_____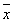乙；s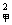
_____s
；
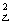（3）请说出此种表示方法的优点．
查看答案和解析>>
科目：初中数学 来源： 题型：
关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2。
（1）求k的取值范围；
（2）如果x1+x2－x1x2＜－1且k为整数，求k的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
小亮和小刚进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡脚跑到坡顶再原路返回坡脚．他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的1．5倍．设两人出发x min后距出发点的距离为y m．图中折线表示小亮在整个训练中y与x的函数关系，其中A点在x轴上，M点坐标为（2，0）．
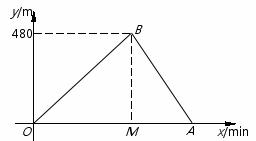
（1）A点所表示的实际意义是 ；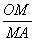
＝ ；
（2）求出AB所在直线的函数关系式；
（3）如果小刚上坡平均速度是小亮上坡平均速度的一半，那么两人出发后多长时间第一次相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
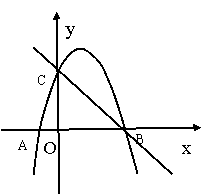
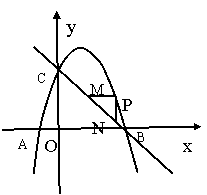
如图，抛物线y=-x2+bx+c交X轴负半轴于点A,交X轴正半轴于点B,交y轴 正半轴于点C，直线BC的解析式为y=kx+3 (k≠0 ), ∠ABC=45 °
⑴求b、c的值；
（2）点P在第一象限的抛物线上,过点P分别作X轴、y轴的平行线,交直线BC 于点M、N,设点P的横坐标为t，线段MN的长为d,求d与t之间的函数关系式（不要求写出自变量t的取值范围)；
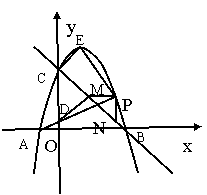
（3）在（2)的条件下，点E为抛物线的顶点，连接EC、EP、AP,AP交y轴于点D，连接DM，若∠DMB=90°，求四边形CMPE的面积.
 | |||||
 |  | ||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，一次函数的解祈式为y=x﹣2；
，解得
，
的结果是_____________ .