
小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
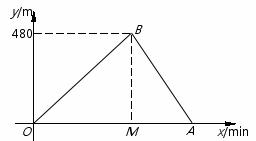
(1)A点所表示的实际意义是 ;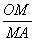 = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
(1)小亮出发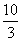 分钟回到了出发点;
分钟回到了出发点; ;
;
(2)y=-360x+1200;
(3)两人第一次相遇时间为2.5min.
【解析】
分析:(1)根据已知M点的坐标进而得出上坡速度,再利用已知下坡的平均速度则是各自上坡平均速度的1.5倍,得出下坡速度以及下坡所用时间,进而得出A点实际意义和OM,AM的长度,即可得出答案;
(2)根据A,B两点坐标进而利用待定系数法求出一次函数解析式即可;
(3)根据小刚上坡平均速度是小亮上坡平均速度的一半首先求出小刚的上坡的平均速度,进而利用第一次相遇两人中小刚在上坡,小亮在下坡,即可得出小亮返回时两人速度之和为:120+360=480(m/min),进而求出所用时间即可.
解:(1)根据M点的坐标为(2,0),则小亮上坡速度为:480÷2=240(m/min),则下坡速度为:240×1.5=360(m/min),
故下坡所用时间为: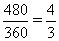 (分钟),
(分钟),
故A点横坐标为:2+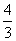 =
=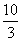 ,纵坐标为0,得出实际意义:小亮出发
,纵坐标为0,得出实际意义:小亮出发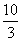 分钟回到了出发点;
分钟回到了出发点;
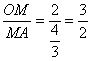 .
.
故答案为:小亮出发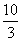 分钟回到了出发点;
分钟回到了出发点; .
.
(2)由(1)可得A点坐标为(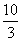 ,0),
,0),
设y=kx+b,将B(2,480)与A(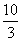 ,0)代入,得:
,0)代入,得:
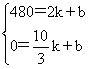 解得k=−360,b=1200.
解得k=−360,b=1200.
所以y=-360x+1200.
(3)小刚上坡的平均速度为240×0.5=120(m/min),
小亮的下坡平均速度为240×1.5=360(m/min),
由图象得小亮到坡顶时间为2分钟,此时小刚还有480-2×120=240m没有跑完,两人第一次相遇时间为2+240÷(120+360)=2.5(min).
【难度】一般


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
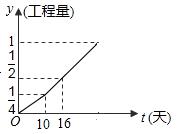
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程。设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少__________天.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知A (4,a),B (﹣2,﹣4)是一次函数y=kx+b的图象和反比例函数y=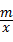 的图象的交点.
的图象的交点.
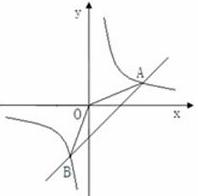
(1)求反比例函数和一次函数的解祈式;
(2)求△A0B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
把一张边长为40 cm的正方形硬纸板,进行适当的裁剪,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余 部分折成一个无盖的长方体盒子.
部分折成一个无盖的长方体盒子.
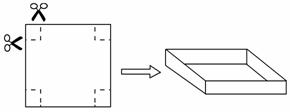

①要使折成的长方体盒子的底面积为484 cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为550 cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
向阳村2010年的人均年收入为12000元,2012年的人均年收入为14520元,设人均年收入 的平均增长率为X,则下列所列的方程中正确的是( ).
(A) 14520(l-x)2=12000 (B) 12000(l+x)2=14520
(C) 12000(l+x2)=14520 (D) 12000(l-x)2=14520
查看答案和解析>>
科目:初中数学 来源: 题型:
小明的爸爸用24000元买进甲、乙两种股票,在甲种股票上涨15%,乙种股票下跌10%时 全部卖出,共获利1350元.
(1) 请问小明爸爸购买甲、乙两种股票各用多少元?
(2)若小明爸爸仍用24000进行投资,在甲、乙两种股票涨幅、跌幅不变的情况下,要获得利 润不低于1500元,那么小明爸爸购买甲种股票至少要用多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com