
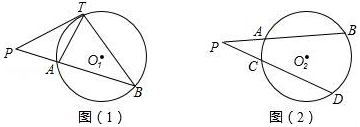
分析 (1)利用弦切角定理和相似三角形的判断方法即可证明△PTA∽△PBT;
(2)如图2中,过点P作⊙O的切线PT,切点是T,根据PT2=PA•PB=PC•PD,求出PD即可解决问题.
解答 解:
(1)∵PT与⊙O1相切于点T,
∴∠PTA=∠B,
∵∠P=∠P,
∴△PTA∽△PBT;
(2)如图2中,过点P作⊙O的切线PT,切点是T.
∵PT2=PA•PB=PC•PD,
∵PA=2,PB=7,PC=3,
∴2×7=3×PD,
∴PD=$\frac{14}{3}$
∴CD=PD-PC=$\frac{14}{3}$-3=$\frac{5}{3}$.
点评 本题考查相似三角形的判定和性质、切线的性质等知识,解题的关键是理解题意,学会利用新知解决未知,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
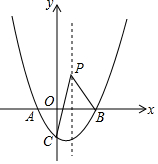 已知抛物线y=x2-2x-3与x轴交于点A、B,与y轴交于点C,P是抛物线对称轴上的一个动点,则当|PB-PC|达到最大值时,点P的坐标为(1,-6).
已知抛物线y=x2-2x-3与x轴交于点A、B,与y轴交于点C,P是抛物线对称轴上的一个动点,则当|PB-PC|达到最大值时,点P的坐标为(1,-6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ③④ | B. | .②④ | C. | ①④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
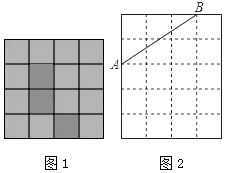 (1)如图1是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形 (涂一个即可);
(1)如图1是4×4的正方形网格,再把其中一个白色小正方形涂上阴影,使整个阴影部分成为轴对称图形 (涂一个即可);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com