
 甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )
甲乙都从A地出发到达B地,甲先出发0.6小时.如图所示描述两人的路程和时间的函数关系,下列说法正确的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①由乙0.4小时行驶了10千米,结合乙在行驶了20千米后改速,即可算出乙改速时的时间,①正确;②根据甲的速度不变,即可算出甲行驶10千米、22千米的时间,二者做差即可得出两次相遇间隔时间,②错误;③根据第二次相遇的时间以及乙改速时的时间,即可得出乙改速后从20千米到22千米用的时间,以及“速度=路程÷时间”即可算出乙改速后的速度,再由“时间=路程÷速度”即可算出乙到达B地的时间,用其减去甲到达B地的时间再减去0.6即可得出结论,③错误;④根据“平均速度=两地间距÷行驶时间”,算出甲乙的平均速度,二者做差即可得出结论,④正确.综上即可得知正确的结论有2个.
解答 解:①(20÷10)×(1-0.6)+1=1.4(小时),
乙在1.4小时后改变速度,①正确;
②甲的速度为:10÷1=10(千米/小时),
甲乙第二次相遇的时间为:22÷10=2.2(小时),
甲乙两次相遇间隔为:2.2-1=1.2(小时),②错误;
③乙改速后的速度为:(22-20)÷(2.2-1.4)=2.5(千米/小时);
甲到达B地的时间为:30÷10=3(小时),
乙到达B地的时间为:(30-20)÷2.5+1.4=5.4(小时),
行驶完全程,乙比甲多用的时间为:5.4-3-0.6=1.8(小时),③错误;
④乙的平均速度为:30÷(5.4-0.6)=6.25(千米/小时),
两人的平均速度差为:10-6.25=3.75(千米/小时),④正确.
综上可知:①④结论正确.
故选C.
点评 本题考查了函数图象,解题的关键是结合函数图象逐条分析4条结论.本题属于中档题,难度不大,解决该题型题目时,根据函数图象找出数据,再根据数量关系列式计算是关键.


科目:初中数学 来源: 题型:选择题
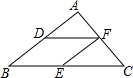 在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )
在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )
如图所示,梯形ABCD的面积为S,AB∥CD,CD=a,AB=b(a<b),对角线AC,BD交于点O,△BOC面积为$\frac{1}{5}$S,则$\frac{a}{b}$=( )| A. | $\frac{3-\sqrt{5}}{3}$ | B. | $\frac{3-\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤0,y≠0 | B. | x≤0,y为一切实数 | C. | x<0,y≠0 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
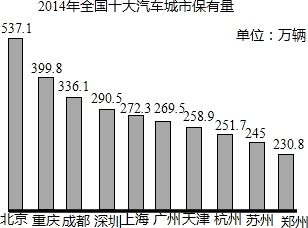 2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.
2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.| a | 1 | 2 | 3 |
| s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com