
【题目】如图,△ABC中,∠B =∠C,点D、E分别是边AB、AC上的点,PD平分∠BDE交BC于H,PE平分∠DEC交BC于G,DQ平分∠ADE交PE延长线于Q。

(1)∠A+∠B+∠C+∠P +∠Q = °;
(2)猜想∠P与∠A的数量关系,并证明你的猜想;
(3)若∠EGH =112°,求∠ADQ 的大小。
【答案】(1)270°;(2)∠P=90°-![]() ∠A,理由见解析;(3)∠ADQ=22°
∠A,理由见解析;(3)∠ADQ=22°
【解析】
(1)由三角形内角和可知∠A+∠B+∠C=180°,由三角形内角和及角平分线的定义可求出∠P +∠Q =90°;
(2)由PD平分∠BDE,PE平分∠DEC,可得![]() ,∠PED=
,∠PED=![]() ,在△PDE中,∠P=180°-∠PDE-∠PED,在△ABC中,ADE+∠AED=180°-∠A ,整理可得∴
,在△PDE中,∠P=180°-∠PDE-∠PED,在△ABC中,ADE+∠AED=180°-∠A ,整理可得∴![]() ;
;
(3)由角平分线的定义及三角形外角的性质可得∠DHG=∠B+∠HDB,∠EGH=∠C+∠GEC,从而∠DHG -∠HDE=∠EGH-∠GED,结合四边形内角和可求∠DHG+∠GED =∠HDE+∠EGH=180°, 进而可得∠HDE=68°,然后根据角平分线的定义及邻补角的定义即可求出∠ADQ 的大小.
解:(1)∵PD平分∠BDE,DQ平分∠ADE,
∴![]() ,∠ADQ=
,∠ADQ=![]() ,
,
∴∠PDE+∠ADQ=![]() (∠BDE+∠ADE)=90°,
(∠BDE+∠ADE)=90°,
∴∠P+∠Q=190°-90°=90°.
∵∠A+∠B+∠C=180°,
∴∠A+∠B+∠C+∠P +∠Q =270°;
(2)猜想![]() ,证明如下:
,证明如下:
∵PD平分∠BDE,PE平分∠DEC
∴![]() ,
,![]()
又在△PDE中,∠P=180°-∠PDE-∠PED=![]()
在△ABC中,∠ADE+∠AED=180°-∠A
∴![]()
(3)∵PD平分∠BDE,PE平分∠DEC,
∴∠HDE=∠HDB,∠GEC=∠GED.
∵∠DHG=∠B+∠HDB,∠EGH=∠C+∠GEC,∠B =∠C,
∴∠DHG -∠HDB=∠EGH-∠GEC,
即∠DHG -∠HDE=∠EGH-∠GED,
∴在四边形DHGE中,∠DHG+∠GED=∠HDE+∠EGH=![]() =180°,
=180°,
∵∠EGH =112°,
∴∠HDE=68°,
∴∠BDE=2∠HDE=136° ,
∴∠ADE=180°-∠BDE =44°.
∵DQ平分∠ADE,
∴∠ADQ=![]() =22°.
=22°.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
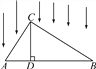
【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
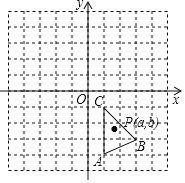
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
(1)将△ABC先向上平移5个单位,再向左平移3个单位,画出平移后得到的△A1B1C1;
(2)写出△A1B1C1各顶点的坐标;
(3)若△ABC内有一点P(a,b),请写出平移后得到的对应点P1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )

A. 点G B. 点E C. 点D D. 点F
查看答案和解析>>
科目:初中数学 来源: 题型:
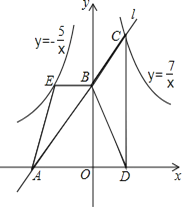
【题目】如图,在平面直角坐标系xOy中,直线l交x轴和y轴于点A,B,反比例函数y=![]() (x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=-
(x>0)的图象于点C,过点C作y轴的平行线交x轴于点D,过点B作x轴的平行线交反比例函数y=-![]() (x<0)的图象于点E,则图中阴影部分的总面积为______.
(x<0)的图象于点E,则图中阴影部分的总面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举办科技比赛,某校参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图如图
(1)该校参加机器人比赛的人数是_____人;“航模”所在扇形的圆心角度数是________°;
(2)补全条形统计图;
(3)从全区参加科技比赛选手中随机抽取80人,其中有16人获奖.今年全区参加科技比赛人数共有3215人,请你估算全区参加科技比赛的获奖人数约是多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
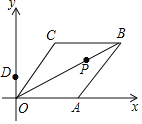
【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4![]() ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
A. (0,0)B. (1,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.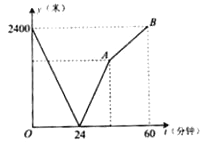
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com