
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.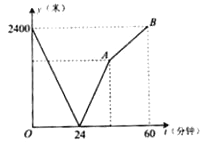
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
【答案】(1)24;40;(2)线段AB的表达式为:y=40t(40≤t≤60)
【解析】(1)根据图象信息,当t=24分钟时甲乙两人相遇,甲60分钟行驶2400米,根据速度=路程÷时间可得甲的速度;
(2)由t=24分钟时甲乙两人相遇,可得甲、乙两人的速度和为2400÷24=100米/分钟,减去甲的速度得出乙的速度,再求出乙从图书馆回学校的时间即A点的横坐标,用A点的横坐标乘以甲的速度得出A点的纵坐标,再将A、B两点的坐标代入,利用待定系数法即可求出线段AB所表示的函数表达式.
(1)根据图象信息,当t=24分钟时甲乙两人相遇,甲的速度为2400÷60=40米/分钟.
(2)∵甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,t=24分钟时甲乙两人相遇,
∴甲、乙两人的速度和为2400÷24=100米/分钟,
∴乙的速度为100-40=60米/分钟.
乙从图书馆回学校的时间为2400÷60=40分钟,
40×40=1600,
∴A点的坐标为(40,1600).
设线段AB所表示的函数表达式为y=kt+b,
∵A(40,1600),B(60,2400),
∴![]() ,解得
,解得![]() ,
,
∴线段AB所表示的函数表达式为y=40t(40≤t≤60).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B =∠C,点D、E分别是边AB、AC上的点,PD平分∠BDE交BC于H,PE平分∠DEC交BC于G,DQ平分∠ADE交PE延长线于Q。

(1)∠A+∠B+∠C+∠P +∠Q = °;
(2)猜想∠P与∠A的数量关系,并证明你的猜想;
(3)若∠EGH =112°,求∠ADQ 的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
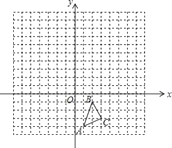
【题目】如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
(1)以O为位似中心,作△A′B′C′∽△ABC,△A′B′C′与△ABC相似比为2:1,且△A′B′C′在第二象限;
(2)在上面所画的图形中,若线段AC上有一点D,它的横坐标为k,点D在A′C′上的对应点D′的横坐标为﹣2﹣k,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G。
DC,连接EF并延长交BC的延长线于点G。
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
科目:初中数学 来源: 题型:
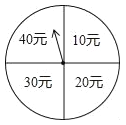
【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
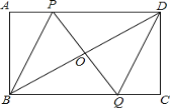
【题目】如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以![]() 的速度向点D 运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
的速度向点D 运动(不与D重合).设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:1.第三组的频数是12.请你回答:
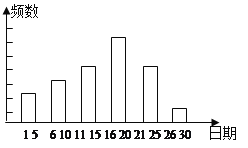
(1)本次活动共有 件作品参赛;
(2)若将各组所占百分比绘制成扇形统计图,那么第四组对应的扇形的圆心角是 度。
(3)本次活动共评出2个一等奖和3个二等奖及三等奖、优秀奖若干名,对一、二等奖作品进行编号并制作成背面完全一致的卡片,背面朝上的放置,随机抽出两张卡片,抽到的作品恰好一个是一等奖,一个是二等奖的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com