
【题目】(12分)为绿化环境,汇川区园林局引进了A、B两种树苗,若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元,问:
(1)A、B两种树苗的单价各是多少?
(2)若计划不超过8300元购进A、B两种树苗共30棵,其中计划A种树苗至少比B种树苗的2倍多2棵,问有几种采购方案?那种方案最节约?
【答案】(1) A树苗每棵300元,B种树苗每棵200元;(2) 有3种方案,其中B种树苗9棵,A种树苗21棵,最节约.
【解析】试题分析:(1)设A种树苗每棵x元,B种树苗每棵y元,根据“若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进A种树苗m棵,则购进B种树苗(30-m)棵,根据购树费用不超过8300元结合A种树苗至少比B种树苗的2倍多2棵,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,从而得出各购树方案,再根据一次函数的性质,即可解决最值问题.
试题解析:
(1)设A种树苗每棵x元,B种树苗每棵y元,则:
![]()
解这个方程组,得: ![]()
答:A树苗每棵300元,B种树苗每棵200元。
(2)解法一:设购进A种树苗m棵,则购进B种树苗(30-m)棵,由题意,得:
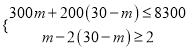
解这个不等式组,得: ![]()
又 m是整数,∴m=21、22或23
故有3种方案:A种树苗21棵,B种树苗9棵
A种树苗22棵,B种树苗8
A种树苗23棵,B种树苗7棵
由购树费用=![]() 知,m最小时最合算,
知,m最小时最合算,
∴ 方案一:A种树苗21棵,B种树苗9棵,最节约
或解法二:设购进B种树苗t棵,则有:
![]()
解得: ![]()
t是整数,∴t=7、8或9
B种树苗9棵,A种树苗21棵,最节约.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
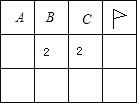
【题目】Windows2000下有一个有趣的游戏“扫雷”,下图是扫雷游戏的一部分:(说明:图中数字2表示在以该数字为中心的8个方格中有2个地雷).小旗表示该方格已被探明有地雷,现在还剩下A、B、C三个方格未被探明,其它地方为安全区(包括有数字的方格)
(1)现在还剩下几个地雷?
(2)A、B、C三个方格中有地雷的概率分别是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数的图象如图所示,以下结论正确的是( )
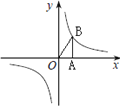
①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=![]() ;
;
④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4).
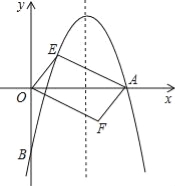
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
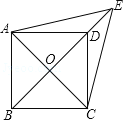
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老板以每颗a元的单价买进水蜜桃100颗,现以每颗比单价多20%的价格卖出80颗后,再以每颗比单价低b元的价格将剩下的20颗卖出,则全部水蜜桃共卖( )
A. [80a+20(a-b)]元
B. [80(1+20%)a+20b]元
C. [100(1+20%)a-20(a-b)]元
D. [80(1+20%)a+20(a-b)]元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com