
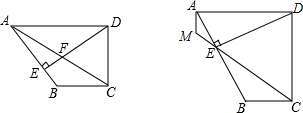
分析 (1)过点B作BH⊥AD于H,如图1,易证四边形BCDH是矩形,从而可求出HD、AH的值,易证△AED∽△AHB,根据相似三角形的性质即可求出AE•AB的值;
(2)延长DE、CB交于点G,如图2,由(1)得:AH=3,AE•AB=18,四边形BCDH是矩形,则有BH=CD=4,根据勾股定理可求出AB,根据AE•AB=18可求出AE,进而可求出EB.由AD∥GC可得△AED∽△BEG,根据相似三角形的性质可求出BG,由此可求出GC.由AD∥GC可得△AFD∽△CFG,根据相似三角形的性质即可求出$\frac{AF}{CF}$;
(3)延长AB、DC交于点N,如图3.由AD∥BC可得△NBC∽△NAD,根据相似三角形的性质可求出NC,由此可求出DN,然后根据勾股定理可求出AN,再运用面积法可求出DE,再根据勾股定理可求出AE,由此可求出EN.由AM∥CD可得△AEM∽△NEC,根据相似三角形的性质即可求出$\frac{ME}{CE}$.
解答 解:(1)过点B作BH⊥AD于H,如图1,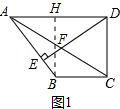
则有∠AHB=∠BHD=90°.
∵AD∥BC,∠BCD=90°,
∴∠ADC=180°-∠BCD=90°,
∴∠BHD=∠HDC=∠BCD=90°,
∴四边形BCDH是矩形,
∴HD=BC=3,
∴AH=AD-HD=6-3=3.
∵DE⊥AB即∠AED=90°,
∴∠AED=∠AHB.
又∵∠EAD=∠HAB,
∴△AED∽△AHB,
∴$\frac{AE}{AH}$=$\frac{AD}{AB}$,
∴AE•AB=AH•AD=3×6=18;
(2)延长DE、CB交于点G,如图2.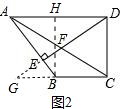
由(1)得:AH=3,AE•AB=18,四边形BCDH是矩形,
则有BH=CD=4,AB=$\sqrt{A{H}^{2}+B{H}^{2}}$=5,
∴AE=$\frac{18}{AB}$=$\frac{18}{5}$,EB=5-$\frac{18}{5}$=$\frac{7}{5}$.
∵AD∥GC,
∴△AED∽△BEG,
∴$\frac{AD}{BG}$=$\frac{AE}{EB}$,
∴$\frac{6}{BG}$=$\frac{18}{7}$,
∴BG=$\frac{7}{3}$,
∴GC=$\frac{7}{3}$+3=$\frac{16}{3}$.
∵AD∥GC,
∴△AFD∽△CFG,
∴$\frac{AF}{CF}$=$\frac{AD}{CG}$=$\frac{6}{\frac{16}{3}}$=$\frac{9}{8}$;
(3)延长AB、DC交于点N,如图3.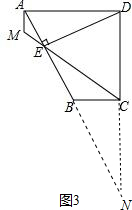
∵AD∥BC,
∴△NBC∽△NAD,
∴$\frac{NC}{ND}$=$\frac{BC}{AD}$,
∴$\frac{NC}{NC+6}$=$\frac{3}{6}$=$\frac{1}{2}$,
解得NC=6,
∴DN=12,
∴AN=$\sqrt{A{D}^{2}+D{N}^{2}}$=6$\sqrt{5}$,
∴DE=$\frac{AD•DN}{AN}$=$\frac{6×12}{6\sqrt{5}}$=$\frac{12\sqrt{5}}{5}$,
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\frac{6\sqrt{5}}{5}$,
∴EN=AN-AE=6$\sqrt{5}$-$\frac{6\sqrt{5}}{5}$=$\frac{24\sqrt{5}}{5}$,
∴$\frac{AE}{EN}$=$\frac{1}{4}$.
∵AM∥CD,
∴△AEM∽△NEC,
∴$\frac{ME}{CE}$=$\frac{AE}{NE}$=$\frac{1}{4}$.
点评 本题主要考查了相似三角形的判定与性质、矩形的判定与性质、勾股定理等知识,通常可以运用相似三角形的性质求线段长、线段比,应熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | 10cm和8cm | B. | 13cm和7cm | C. | 9cm和9cm | D. | 9cm和12cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
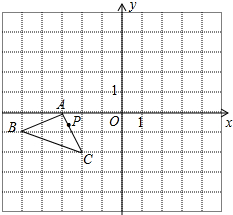 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+5,b+4)
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+5,b+4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示是某战役缴获敌军防御工事坐标地图的碎片,依稀可见:一号暗堡A的坐标为(4,3),五号暗堡B的坐标为(-2,3),另有情报得知敌军指挥部的坐标为(-3,-2).请你在图中画出直角坐标系,并且标示出敌军指挥部的位置.
如图所示是某战役缴获敌军防御工事坐标地图的碎片,依稀可见:一号暗堡A的坐标为(4,3),五号暗堡B的坐标为(-2,3),另有情报得知敌军指挥部的坐标为(-3,-2).请你在图中画出直角坐标系,并且标示出敌军指挥部的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
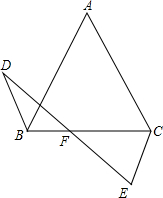 如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.
如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对角分别相等的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 一组对边平行另一组对边相等的四边形是平行四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com