
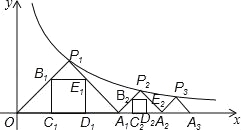
����Ŀ����ͼ����P1��x1��y1������P2��x2��y2����������Pn��xn��yn���ں���y=![]() ��x��0����ͼ���ϣ���P1OA����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA1���ڽ�������B1C1D1E1���ܳ���Ϊl1����P2A1A2���ڽ������ε��ܳ���Ϊl2��������PnAn��1An���ڽ�������BnCnDnEn���ܳ���Ϊln����l1+l2+l3+��+ln= ���ú�n��ʽ�ӱ�ʾ����
��x��0����ͼ���ϣ���P1OA����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA1���ڽ�������B1C1D1E1���ܳ���Ϊl1����P2A1A2���ڽ������ε��ܳ���Ϊl2��������PnAn��1An���ڽ�������BnCnDnEn���ܳ���Ϊln����l1+l2+l3+��+ln= ���ú�n��ʽ�ӱ�ʾ����
���𰸡�![]()
![]()
��������
������������P1��P1M1��x����M1��
��֪M1��1��0����OA1���е㣬
��A1��2��0����
�ɵ�P1������Ϊ��1��1����
��P1O�Ľ���ʽΪ��y=x��
��P1O��A1P2����A1P2�ı���ʽһ����ϵ����ȣ�
��A1��2��0������y=x+b��
��b=��2��
��A1P2�ı���ʽ��y=x��2��
��y=![]() ��x��0�����������P2��1+
��x��0�����������P2��1+![]() ����1+
����1+![]() ����
����
���ϣ�A2��2![]() ��0����
��0����
P3��![]() +
+![]() ����
����![]() +
+![]() ����A3��2
����A3��2![]() ��0����
��0����
�������ƣ���An������Ϊ��2![]() ��0����
��0����
��l1=![]() OA1��l2=
OA1��l2=![]() A1A2��l3=
A1A2��l3=![]() A2A3��ln=
A2A3��ln=![]() An��1An��
An��1An��
��l1+l2+l3+��+ln=![]() OAn=
OAn=![]() ��2
��2![]() =
=![]()
![]() ��
��
�ʴ�Ϊ��![]()
![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
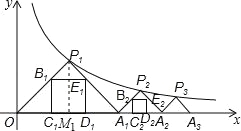
����Ŀ����ͼ��ʾ��ͼ1��ͼ2�ֱ���![]() �����������е�ÿ��С�����εı߳���Ϊ1���밴����Ҫ��ֱ���Ӧ��ͼ�Σ�������ͼ�ε�ÿ�������������С�����εĶ����ϣ�
�����������е�ÿ��С�����εı߳���Ϊ1���밴����Ҫ��ֱ���Ӧ��ͼ�Σ�������ͼ�ε�ÿ�������������С�����εĶ����ϣ�

(1)��ͼ1�л���һ���ܳ�Ϊ![]() ������
������![]() (��������)��
(��������)��
(2)��ͼ2�л���һ�����Ϊ9��ƽ���ı���![]() ��������
��������![]() ����ֱ��д��ƽ���ı���
����ֱ��д��ƽ���ı���![]() ���ܳ���
���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
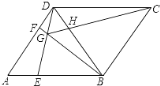
����Ŀ����ͼ��������ABCD�У�tanA= ![]() ����E��F�ֱ���AB��AD������ĵ㣨����˵��غϣ�����AE=DF������BF��DE�ཻ�ڵ�G������CG��BD�ཻ�ڵ�H���������¼������ۣ���1����AED�ա�DFB����2��CG��BDһ������ֱ����3����BGE�Ĵ�СΪ��ֵ����4��S�ı���BCDG=
����E��F�ֱ���AB��AD������ĵ㣨����˵��غϣ�����AE=DF������BF��DE�ཻ�ڵ�G������CG��BD�ཻ�ڵ�H���������¼������ۣ���1����AED�ա�DFB����2��CG��BDһ������ֱ����3����BGE�Ĵ�СΪ��ֵ����4��S�ı���BCDG= ![]() CG2��������ȷ���۵����Ϊ________��
CG2��������ȷ���۵����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() ��
��![]() ��
��
![]() ��һ�κ����ı���ʽ��
��һ�κ����ı���ʽ��
![]() ��P��x���ϣ���
��P��x���ϣ���![]() ��ֵ��Сʱ����ͼ�л�����P���������P�����꣮
��ֵ��Сʱ����ͼ�л�����P���������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж�����ı�����ƽ���ı��ε���

A��AB��DC��AD��BC����B��AB=DC��AD=BC
C��AO=CO��BO=DO�� ��D��AB��DC��AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�BD������һ���Խ��ߣ���A��C������AE��BD��CF��BD������ֱ�ΪE��F���ӳ�AE��CF�ֱ�CD��AB��M��N��
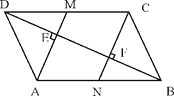
��1����֤���ı���CMAN��ƽ���ı��Ρ�
��2����֪DE��4��FN��3����BN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2016��Ϊ���á�����ƶ����Ͷ���ʽ�1200��Ԫ������ذ��ã����滮Ͷ����ذ����ʽ����ƽ���������������ڱ��ֲ��䣬��֪2018����2016��Ļ�����������Ͷ����ذ����ʽ�1500��Ԫ��
��1��2017��õ�Ͷ����ذ����ʽ�Ϊ����Ԫ��
��2����2017����ذ��õľ���ʵʩ�У��õ�Ҫ��Ͷ���������Ȱ�Ǩ�ⷿ�������ʽ���2017��õ�Ͷ����ذ����ʽ��25%���涨ǰ1000��������1000������ÿ��ÿ�콱��8Ԫ��1000���Ժ�ÿ��ÿ�콱��5Ԫ�����ⷿ400����㣬��2017��õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ��������Σ�
���������![]() ��
��![]() ���ϵĸߣ�������
���ϵĸߣ�������![]() ��һ��
��һ��![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���֪
�ϣ���֪![]() ��
��![]() ��
��

��1����֤��![]() ��
��
��2�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
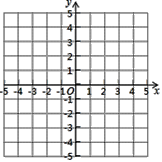
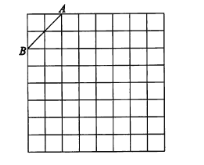
����Ŀ����ͼ���ǹ��Ϊ8��8�������������������������а�����Ҫ�������
(1)�������н���ƽ��ֱ������ϵ��ʹA������Ϊ(-2��4)��B������Ϊ(-4��2)��
(2)��(1)��ǰ���£��ڵڶ������ڵĸ������һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C��������ǣ�
(3)��((2)�С�ABC���ܳ�(�����������)��
(4)����((2)����ABC����y��ԳƵ���A'B'C'.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com