
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
证明:(1)BF=DF.
(2)AE//BD.
(3)若AB=6,BC=8,求AF的长,并求△FBD的周长和面积。

【答案】(1)证明见解析;(2)证明见解析;(3)AF=![]() 周长为22.5;面积为:
周长为22.5;面积为: ![]() .
.
【解析】试题分析:(1)根据平行线的性质和折叠的性质可证得∠DBC=∠ADB,根据等腰三角形的判定即可得BF=DF;(2)先证AF=EF,即可得∠AEF=∠EAF,再证∠AEF=∠FBD,即可判定AE//BD;(3)设AF=x,则DF=BF=8-x,在RtΔABF中,根据勾股定理列出方程,解方程即可求得x的值;在RtΔBDC中,根据勾股定理得BD的长,即可求得△FBD的周长和面积.
试题解析:
(1)矩形ABCD得出AD//BC,∴∠ADB=∠FDB根据对折得,∠FDB=∠DBC
∴∠DBC=∠ADB ∴BF=DF(等边对等角)
(2)∵AD=BC=BE,BF=DF
∴AD-DF=BE-BF 即AF=EF
∴∠AEF=∠EAF
又∵∠AEF+∠EAF=∠ADB+∠FBD
∴∠AEF=∠FBD
∴AE//BD
(3)设AF=x,则DF=BF=8-x
在RtΔABF中,AF2+AB2=BF2 即62+x2=(8-x)2 解得x=![]() .
.
在RtΔBDC中,根据勾股定理得:BD=10,
所以,三角形FBD的周长为10+2FD=10+![]() =22.5
=22.5
三角形FBD的面积为S=![]() ×6×
×6×![]() =
=![]()


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】2017年6月13日,2016——2017赛季NBA总决赛第五场金州勇士队129:120战胜克利夫兰骑士队,赢得了总冠军,凯文·杜兰特表现抢眼,荣膺总决赛MVP,总决赛中凯文·杜兰特和勒布朗·詹姆斯每场得分数据如下:
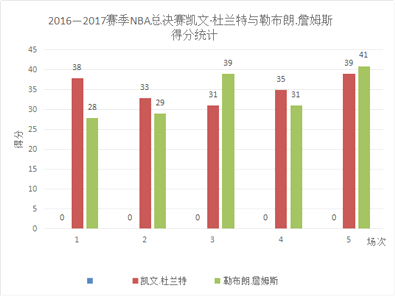
(1)求两名队员得分数的平均数.
(2)求凯文·杜兰特五场比赛得分的中位数.
(3)篮球迷小明同学已经求出了勒布朗·詹姆斯五场得分的方差为S2=28.64,凯文·杜兰特五场比赛得分的方差为S2=8.96,请帮他说明哪位运动员发挥更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列抛物线中,与x轴有两个交点的是( )
A. y=3x2-5x+3 B. y=4x2-12x+9 C. y=x2-2x+3 D. y=2x2+3x-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中,移项正确的是( )
A. 由x-3=4得x=4-3
B. 由2=3+x得2-3=x
C. 由3-2x=5+6得2x-3=5+6
D. 由-4x+7=5x+2得5x-4x=7+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球被抛出后,距离地面的高度h(m)和飞行时间t(s)满足下面函数解析式:h=-5t2+10t+1,则小球距离地面的最大高度是________m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com