
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,-1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
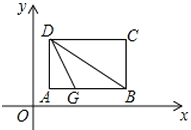
【答案】(1)AG=1.5;AM+CM最小值为![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据折叠的性质可得AG=GH,设AG的长度为x,在Rt△HGB中,利用勾股定理求出x的值;
(2)作点A关于直线y=-1的对称点A',连接CA'与y=-1交于一点,这个就是所求的点,求出此时AM+CM的值;
(3)求出G、H的坐标,然后设出解析式,代入求解即可得出解析式.
试题解析:(1)由折叠的性质可得,AG=GH,AD=DH,GH⊥BD,
∵AB=4,BC=3,
∴BD=![]() ,
,
设AG的长度为x,
∴BG=4-x,HB=5-3=2,
在Rt△BHG中,GH2+HB2=BG2,
x2+4=(4-x)2,
解得:x=1.5,
即AG的长度为1.5;
(2)如图所示:作点A关于直线y=-1的对称点A',连接CA'与y=-1交于M点,
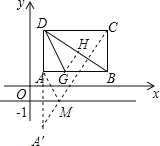
∵点B(5,1),
∴A(1,1),C(5,4),A'(1,-3),
AM+CM=A'C=![]() ,
,
即AM+CM的最小值为![]() ;
;
(3)∵点A(1,1),
∴G(2.5,1),
过点H作HE⊥AD于点E,HF⊥AB于点F,如图所示,
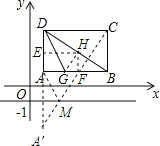
∴△AEH∽△DAB,△HFB∽△DAB,
∴![]() ,
, ![]() ,
,
即![]() ,
, ![]() ,
,
解得:EH=![]() ,HF=
,HF=![]() ,
,
则点H(![]() ,
, ![]() ),
),
设GH所在直线的解析式为y=kx+b,
则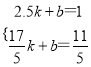 ,解得:
,解得: 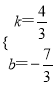 ,
,
则解析式为: ![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2﹣14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.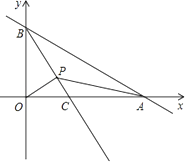
(1)求OA,OB的长;
(2)设△APB和△OPB的面积分别为s1 , s2 , 求s1:s2;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,直接写出时间t;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面几种三角形:
①有两个角为60°的三角形;
②三个外角都相等的三角形;
③一条边上的高也是这条边上的中线的三角形;
④有一个角为60°的等腰三角形.
其中是等边三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有员工50人,为了提高经济效益,决定引进一条新的生产线并从现有员工中抽调一部分员工到新的生产线上工作,经调查发现:分工后,留在原生产线上工作的员工每月人均产值提高40%;到新生产线上工作的员工每月人均产值为原来的3倍,设抽调x人到新生产线上工作.
(1)填空:若分工前员工每月的人均产值为a元,则分工后,留在原生产线上工作的员工每月人均产值是元,每月的总产值是元;到新生产线上工作的员工每月人均产值是元,每月的总产值是元;
(2)分工后,若留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半.问:抽调的人数应该在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形的周长为36m,矩形绕着它的一条边旋转形成一个圆柱,设矩形的一条边长为xm,圆柱的侧面积为ym2 , 则y与x的函数关系式为( )
A.y=﹣2πx2+18πx
B.y=2πx2﹣18πx
C.y=﹣2πx2+36πx
D.y=2πx2﹣36πx
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,如果ɑ,β都为锐角,且tanɑ=![]() ,tanβ=
,tanβ=![]() ,则ɑ+β=___________;
,则ɑ+β=___________;
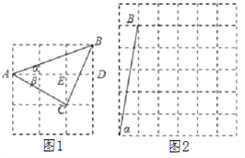
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ=![]() 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON,使得∠MON=ɑ-β.此时ɑ-β=__________度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON,使得∠MON=ɑ-β.此时ɑ-β=__________度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com