
分析 根据根与系数的关系即可得出x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$.
(1)利用通分以及配方法将$\frac{{x}_{2}}{{x}_{1}}+\frac{{x}_{1}}{{x}_{2}}$变形为$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}}$,再代入x1+x2=-$\frac{3}{2}$、x1•x2=-$\frac{1}{2}$即可算出结果;
(2)利用通分以及配方法将$\frac{{x}_{2}}{{x}_{1}+1}+\frac{{x}_{1}}{{x}_{2}+1}$变形为$\frac{({x}_{1}+{x}_{2})^{2}+({x}_{1}+{x}_{2})-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}+({x}_{1}+{x}_{2})}$,再代入x1+x2=-$\frac{3}{2}$、x1•x2=-$\frac{1}{2}$即可算出结果.
解答 解:∵方程2x2+3x-1=0的两根为x1和x2,
∴x1+x2=-$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$.
(1)$\frac{{x}_{2}}{{x}_{1}}+\frac{{x}_{1}}{{x}_{2}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}•{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{(-\frac{3}{2})^{2}-2×(-\frac{1}{2})}{-\frac{1}{2}}$=-$\frac{13}{2}$;
(2)$\frac{{x}_{2}}{{x}_{1}+1}+\frac{{x}_{1}}{{x}_{2}+1}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}+{(x}_{1}+{x}_{2})}{{x}_{1}•{x}_{2}+({x}_{1}+{x}_{2})}$=$\frac{({x}_{1}+{x}_{2})^{2}+({x}_{1}+{x}_{2})-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}+({x}_{1}+{x}_{2})}$=$\frac{(-\frac{3}{2})^{2}+(-\frac{3}{2})-2×(-\frac{1}{2})}{-\frac{1}{2}+(-\frac{3}{2})}$=-$\frac{7}{8}$.
点评 本题考查了根与系数的关系,解题的关键是:(1)将原式变形为$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}}$;(2)将原式变形为$\frac{({x}_{1}+{x}_{2})^{2}+({x}_{1}+{x}_{2})-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}+({x}_{1}+{x}_{2})}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.
在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
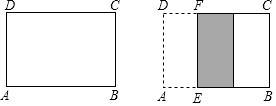 如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).
如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).| x/cm | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| S/cm2 | 10 | 30 | 50 | 70 | 60 | 40 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
如图,在平面直角坐标系中,O为坐标原点,抛物线F:y=ax2+2ax+c经过A(-4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com