
【题目】如图:已知在△ABC中,∠ACB=90°,AC=BC=1,点D是AB上任意一点,AE⊥AB,且AE=BD,DE与AC相交于点F. 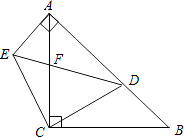
(1)试判断△CDE的形状,并说明理由.
(2)是否存在点D,使AE=AF?如果存在,求出此时AD的长,如果不存在,请说明理由.
【答案】
(1)解:△CDE是等腰直角三角形.理由如下:
∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵AE⊥AB,
∴∠CAE=90°﹣45°=45°,
∴∠B=∠CAE,
在△ACE和△BCD中, 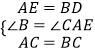 ,
,
∴△ACE≌△BCD(SAS),
∴CD=CE,∠ACE=∠BCD,
∵∠ACD+∠BCD=∠ACB=90°,
∴∠DCE=∠ACD+∠ACE=90°,
∴△CDE是等腰直角三角形
(2)解:存在AD=1.理由如下:
∵AE=AF,∠CAE=45°,
∴∠AEF=∠AFE= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠ADE=90°﹣67.5°=22.5°,
∵△CDE是等腰直角三角形,
∴∠CDE=45°,
∴∠ADC=22.5°+45°=67.5°,
在△ACD中,∠ACD=180°﹣45°﹣67.5°=67.5°,
∴∠ACD=∠ADC,
∴AD=AC=1.
【解析】(1)根据等腰直角三角形的性质求出∠B=∠BAC=45°,再求出∠CAE=45°,从而得到∠B=∠CAE,再利用“边角边”证明△ACE和△BCD全等,根据全等三角形对应边相等可得CD=CE,全等三角形对应角相等可得∠ACE=∠BCD,再求出∠DCE=90°,从而得解;(2)根据等腰三角形两底角相等求出∠AEF=∠AFE=67.5°,再根据直角三角形两锐角互余求出∠ADE=22.5°,然后求出∠ADC=67.5°,利用三角形的内角和定理求出∠ACD=67.5°,从而得到∠ACD=∠ADC,根据等角对等边即可得到AD=AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人连续7年调查某县养鸡业的情况,提供了两方面的信息图(如图).甲调查表明:养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只;乙调查表明:养鸡场的个数由第1年的46个减少到第7年的22个.现给出下列四个判断:①该县第2年养鸡场产鸡的数量为1.3万只;②该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量;③该县这7年养鸡场产鸡的数量逐年增长;④这7年中,第5年该县养鸡场出产鸡的数量最多.根据甲、乙两人提供的信息,可知其中正确的判断有( )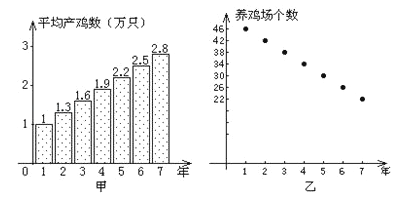
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(﹣2,1)与点B关于原点对称,则点B的坐标为( )
A.(﹣2,1)
B.(2,﹣1)
C.(2,1)
D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图:

请你根据以上的信息,回答下列问题:
(1) 本次共调查了_____名学生,其中最喜爱戏曲的有_____人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是______;
(2) 根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com