
����Ŀ����1����ͼ1���߶�OA��һ���˵�O��ֱ��l�ϣ�����ֱ��l���ɵ����Ϊ50������OAΪһ�����������Σ�����ʹ��һ������P��ֱ��l�ϣ������ĵ����������ܻ��� ������

��2����ͼ1�����OA��ֱ��l���ɵ����Ϊ60������OAΪһ�����������Σ�����ʹ��һ������P��ֱ��l�ϣ������ĵ����������ܻ��� ������
��һ�룺��ͼ2����ABC�У���A��20������B��50����������C��һ��ֱ�ߣ��ָ��һ������������������ֱ�������Ի��� ������
��һ�㣺��ͼ3������ABC�У���BAC��20���������ڹ���C��һ��ֱ�ߣ��ܰѸ������ηֳ��������������Σ������B�Ķ�����
���𰸡���1��4����2��2;��һ�룺 4����һ�㣺70����40����100����
��������
��1�����ݵ��������ε��ж�����������ȵ��������ǵ��������μ��ɵõ����ۣ�
��2����OΪԲ�ģ�OAΪ�뾶��������ֱ��l�����㣬���ɵõ����ۣ�
��һ�룺������������ٵ�AC=AF���ڵ�BC=BE���۵�CB=CG���ܵ�AD��CD�����ǵõ����ۣ�
��һ�㣺��ͼ3����AD=CD��������������ٵ�CD=BDʱ����B=��BCD=70�����ڵ�CD=BCʱ����B=��CDB=40�����۵�BD=BCʱ����B=180��-40��-40��=100������ͼ4����AC=AE��CE=BEʱ��G���ݵ��������ε����ʼ��ɵõ����ۣ�
�⣺��1����ͼ1���ٵ�AO��OP1���ڵ�AO��AP2���۵�AO��OP3���ܵ�AP4��OP4�������ĵ����������ܻ�4����
�ʴ�Ϊ��4��

��2����OΪԲ�ģ�OAΪ�뾶��������ֱ��l�����㣻
�������ĵ����������ܻ�2����
�ʴ�Ϊ��2��
��һ�룺�ٵ�AC��AF���ڵ�BC��BE���۵�CB��CG���ܵ�AD��CDʱ��������C��һ��ֱ�ߣ��ָܷ��һ�����������Σ�
�������C��һ��ֱ�ߣ��ָ��һ������������������ֱ�������Ի�4����

�ʴ�Ϊ��4��
��һ�㣺��ͼ3����AD��CD��

���ACD����A��20����
���CDB��40����
��ٵ�CD��BDʱ����B����BCD��70����
�ڵ�CD��BCʱ����B����CDB��40����
�۵�BD��BCʱ����B��180����40����40����100����
��ͼ4����AC��AE��CE��BEʱ��

�ߡ�A��20����
���ACE����AEC��80����
���B����BCE��40����
�������������ڹ���C��һ��ֱ�ߣ��ܰѸ������ηֳ��������������Σ���B�Ķ���Ϊ70����40����100����


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l����O�����ڵ�A����P��ֱ��l�ϣ�ֱ��PO����O�ڵ�B��C��OD��AB������ΪD����PA�ڵ�E��
��1���ж�ֱ��BE����O��λ�ù�ϵ����˵�����ɣ�
��2����PB=OB=6����AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��a�dz�����a��0�������н�����ȷ���ǣ� ��
��a�dz�����a��0�������н�����ȷ���ǣ� ��
A����a=1ʱ������ͼ���㣨��1��1��
B����a=��2ʱ������ͼ����x��û�н���
C����a��0������ͼ��Ķ���ʼ����x����·�
D����a��0����x��1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB = AC���ڡ�ABC���ⲿ���ȱ������Ρ�ABD��EΪAB���е㣬���� DE���ӳ���BC�ڵ�F.
(1)��ͼ1������BAC = 90�㣬����CD����֤��CDƽ�֡�ADF��
(2)��ͼ2������A�۵���CAD��ʹ��C���D�غϣ��ۺ�AM��EF�ڵ�M������M�����ڡ�ABC��ƽ�����ϣ�����BM���ӳ���AC�ڵ�N������������ѧϰС��ֱ�ó������������ۣ��١�BAC�Ķ�����һ����ֵ��Ϊ100�㣻���߶�MN��NCһ�����.
����ѡ������һ�����ۣ��ж��Ƿ���ȷ?����ȷ������֤��:������ȷ��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ�ȥ��8�µ�����һ���ľ�1160����Ԥ����9�·ݽ��������������۸�Ϊÿ��10Ԫ�����ۼ�Ϊ12Ԫ/�������ȫ���۳�����ÿ�Ǽ�0.1Ԫ���������ͼ���2����
��1������ľߵ���9�·�������������1100�������ۼ�Ӧ�����ڶ���Ԫ��
��2�����������ã�10�·ݸ��ľ߽��۱�8�µĽ���ÿ������20%���õ��������˽�����������ǿ���������ȣ����10�·ݵ���������9�·��ڣ�1���������µ����������������m%�����ۼ۱�9�·��ڣ�1���������µ�����ۼۼ���![]() m%�����10�·�����ﵽ3388Ԫ����m��ֵ��m��10����
m%�����10�·�����ﵽ3388Ԫ����m��ֵ��m��10����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,���κ���y=ax2+bx+c��a��0����ͼ���㣨1,2������x�ύ��ĺ�����ֱ�Ϊx1��x2�����Щ�1��x1��0.1��x2��2.���н��ۣ�4a+2b+c��0��2a+b��0��b2+8a��4ac��
a����1�����н�����ȷ���У� ��
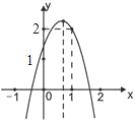
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��

��1����֤��OE=OF��
��2����CE=12��CF=5����OC�ij���
��3������O�ڱ�AC���˶���ʲôλ��ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��Ϊ10������O��λ��ֱ��AB������ж���C�Ͷ���P����֪BC��CA=4��3����P�ڰ�Բ��AB���˶�������A��B�����غϣ�������C��CP�Ĵ���CD��PB���ӳ�����D�㣮

��1����֤��ACCD=PCBC��
��2������P�˶���AB���е�ʱ����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽������ͼ1���߳�Ϊa�Ĵ�����������һ���߳�Ϊb��С�����Σ���ͼ1�е���Ӱ����ƴ��һ�������Σ���ͼ2��ʾ����ͨ���۲�Ƚ�ͼ2��ͼ1�е���Ӱ������������Եõ��˷���ʽ�� �������ú�a��b�ĵ�ʽ��ʾ��
��Ӧ�ã���Ӧ�������ʽ������и��⣺
��1����֪4m2��12+n2��2m+n��4����2m��n��ֵΪ�� ����
��2�����㣺20192��2020��2018��
����չ�����㣺1002��992+982��972+��+42��32+22��12��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com