
【题目】我市计划对某地块的1000m2区域进行绿化,由甲、乙两个工程队合作完成.已知甲队每天能完成绿化的面积是乙队的2倍;若两队分别各完成300m2的绿化时,甲队比乙队少用3天.
(1)求甲、乙两工程队每天能完成的绿化的面积;
(2)两队合作完成此工程,若甲队参与施工x天,试用含x的代数式表示乙队施工的天数y;
(3)若甲队每天施工费用是0.6万元,乙队每天为0.2万元,且要求两队施工的天数之和不超过16天,应如何安排甲、乙两队施工的天数,才能使施工总费用最低?并求出最低费用时的值.
【答案】(1)甲、乙两工程队每天能完成的面积分别是100m2、50m2;
(2)y==20-2x;
(3)甲施工4天,乙施工12天时施工总费用最低,最低费用是4.8万元
【解析】试题分析:(1)、设乙工程队每天能完成绿化的面积是xm2,根据天数之间的关系列出分式方程,从而得出答案;(2)、根据总量为1000,得出y与x的关系式;(3)、根据x+y≤16得出x的取值范围,然后列出总费用与x的函数关系式,根据一次函数的性质得出最小值.
试题解析:(1)设乙工程队每天能完成绿化的面积是xm2,根据题意得:![]() -
-![]() =3
=3
解得:x=50 经检验,x=50是原方程的解且符合题意
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成的面积分别是100m2、50m2;
(2)由题意得:100x+50y=1000, 即:y=![]() =20-2x
=20-2x
(3)由(2)可得y=20-2x ∵x+y≤16, ∴x+20-2x≤16, ∴x≥4
记总费用为W元
W=0.6x+0.2(20-2x)=0.2x+4 ∵0.2>0,所以w随着x的增加而增加
∴当x=4时, 此时y=20-2x=12 W最少=0.2×4+4=4.8万元
即甲施工4天,乙施工12天时施工总费用最低,最低费用是4.8万元.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】a,b是有理数,它们在数轴上的对应点的位置如图所示:把a,﹣a,b,﹣b按照从小到大的顺序排列( ) ![]()
A.﹣b<﹣a<a<b
B.a<﹣b<b<﹣a
C.﹣b<a<﹣a<b
D.a<﹣b<﹣a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: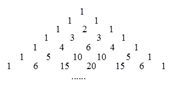
(1)图中给出了七行数字,根据构成规律,第8行中从左边数第3个数是;
(2)利用不完全归纳法探索出第n行中的所有数字之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(x﹣1)(2x+1)﹣(x2+x﹣2)的结果,与下列哪一个式子相同( )
A.x2﹣2x﹣3
B.x2﹣2x+1
C.x2+x﹣3
D.x2﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com