
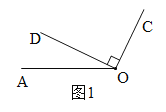
����Ŀ����ͼ��ֱ��l����A��B���㣬��O���߶�AB�ϵ�һ�㣬��OA=10cm��OB=5cm��
��1������C���߶� AB ���е㣬���߶�CO�ij���
��2�������� P��Q �ֱ�� A��B ͬʱ�����������˶�����P���ٶ�Ϊ4cm/s����Q���ٶ�Ϊ3cm/s�����˶�ʱ��Ϊ x �룬
�ٵ� x=__________��ʱ��PQ=1cm��
������M�ӵ�O��7cm/s���ٶ���P��Q����ͬʱ�����˶����Ƿ���ڳ���m��ʹ��4PM+3OQ��mOMΪ��ֵ�������������mֵ�Լ������ֵ���������ڣ���˵�����ɣ�
��3�������������� OC��OD ��������OAͬʱ�Ƶ�O˳ʱ�뷽����ת��OC��ת���ٶ�Ϊ6��/�룬OD ��ת���ٶ�Ϊ2��/��.��OC��OD��һ���غ�ʱ��OC��OD ͬʱֹͣ��ת������תʱ��Ϊt�룬��tΪ��ֵʱ������ OC��OD��

���𰸡���1��CO=2.5����2����14��16 ���ڶ�ֵ55�����ɼ���������3��t=22.5��67.5
��������
��1��������߶�AB�ij���Ȼ������߶��е�Ķ�������
��2������PQ=1���õ�|15-��4x-3x��|=1���ⷽ�̼��ɣ�
���ȱ�ʾ��PM��OQ��OM�ij�������4PM+3OQ��mOM�õ�55+��21-7m��x��Ҫʹ4PM+3OQ��mOMΪ��ֵ����21-7m=0���ⷽ�̼��ɣ�
��3��������������ۣ�����ͼ�Σ�����ͼ���г����̣��ⷽ�̼��ɣ�
��1����OA=10cm��OB=5cm����AB=OA+OB=15cm��
����C���߶� AB ���е㣬��AC=![]() AB=7.5cm����CO=AO-AC=10-7.5=2.5��cm����
AB=7.5cm����CO=AO-AC=10-7.5=2.5��cm����
��2���١�PQ=1����|15-��4x-3x��|=1����|15-x|=1����15-x=��1����ã�x=14��16��
�ڡ�PM=10+7x-4x=10+3x��OQ=5+3x��OM=7x����4PM+3OQ��mOM=4��10+3x��+3��5+3x��-7mx=55+��21-7m��x��Ҫʹ4PM+3OQ��mOMΪ��ֵ����21-7m=0����ã�m=3����ʱ��ֵΪ55��
��3���������������������ͼ1�������������6t-2t=90�������t=22.5��
����ͼ2�������������6t+90=360+2t�������t=67.5��
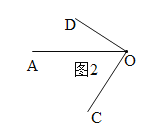
������������t=22.5���67.5��ʱ������ OC��OD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ����Rt��ABC�У���ACB=90����BAC=30�㣮
���ֲ�������1������ֱ�DZ�AC���ڵ�ֱ��Ϊ�Գ��ᣮ��Rt��ABC����ԳƱ任��������ԭͼ���������ĶԳ�ͼ�Σ�
�۲췢�֣���2��Rt��ABC�����ĶԳ�ͼ�������ʲôͼ�Σ�����ȷ���ж����� ����
������������3�����������ͼ�Σ��������ֱ�DZ�BC��б��AB��������ϵ����֤����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��![]() �ֱ���x�ᡢy�ύ�ڵ�B��C������ֱ��l2��
�ֱ���x�ᡢy�ύ�ڵ�B��C������ֱ��l2��![]() ���ڵ�A��
���ڵ�A��
��1�������A������
��2����D���߶�OA�ϵĵ㣬�ҡ�COD�����Ϊ12����ֱ��CD�Ľ���ʽ
��3���ڣ�2���������£���P������CD�ϵĵ㣬��ƽ�����Ƿ���ڵ�Q��ʹ��O��C��P��QΪ������ı��������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������н���һ���ɱ�Ϊ8Ԫ/�����ľߺУ����鷢�֣������ľߺ�ÿ�����ڵ�������y�����������Ķ���x��Ԫ/�����Ĺ�ϵ��ͼ��ʾ�� 
��1���������ľߺ�ÿ�����ڵ�������y�����������Ķ���x��Ԫ/����֮��ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ����
��2��ÿ���ľߺж����Ƕ���Ԫʱ������ÿ�������������ľߺУ��������������أ��ɻ�õ�������ߣ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2011��5��22�թ�29�����������ൺ�о������յ�������ë����������������ڱ����У�ij����ë����˶�·�߿��Կ�����������y=�� ![]() x2+bx+c��һ���֣���ͼ�������г����B�����O��ľ�����1m������ص�A��O��ľ�����4m����ô���������ߵĽ���ʽ�ǣ�������
x2+bx+c��һ���֣���ͼ�������г����B�����O��ľ�����1m������ص�A��O��ľ�����4m����ô���������ߵĽ���ʽ�ǣ������� 
A.y=�� ![]() x2+
x2+ ![]() x+1
x+1
B.y=�� ![]() x2+
x2+ ![]() x��1
x��1
C.y=�� ![]() x2��
x2�� ![]() x+1
x+1
D.y=�� ![]() x2��
x2�� ![]() x��1
x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ˮƽ����ߣ����ýγ�Խ��Խ��ؽ����ͥ��С����������һ��С�γ�����������¼��7����ÿ����ʻ��·�̣����������50kmΪ��������50km�ļ�Ϊ��+��������50km�ļ�Ϊ���������պ�50km�ļ�Ϊ��0����
��һ�� | �ڶ��� | ������ | ������ | ������ | ������ | ������ | |
·�̣�km�� | ��8 | ��11 | ��14 | 0 | ��16 | +41 | +8 |
��1�������������ƽ��ÿ����ʻ����ǧ�ף�
��2����ÿ��ʻ100km��������6�������ͼ�6.2Ԫ/���������С����һ���£���30��ƣ������ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��F��G��H�ֱ��DZ�AB��DC��BC��AD�ϵĵ㣬��AE��CF��BG��DH.��֤��EF��GH����ƽ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������a��b��c�������ϵ�λ����ͼ��ʾ�������x��һԪ���η���ax2+bx+c=0��������ǣ� �� ![]()
A.��������ȵ�ʵ����
B.����������ȵ�ʵ����
C.��ʵ����
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������MΪ���������ABC������һ�㣬����AM��BM��CM����ABΪһ���������ȱ���������ABE����BM�Ƶ�B��ʱ����ת60���õ�BN������EN��
��1����֤����AMB�ա�ENB��
��2����AM+BM+CM��ֵ��С����Ƶ�MΪ��ABC�ķ����㣮����MΪ��ABC�ķ����㣬�����ʱ��AMB����BMC����CMA�Ķ�����
��3��С���������������õ�һ������������η�����ļ�㷽������ͼ�����ֱ�����ABC��AB��ACΪһ���������ȱ���ABE�͵ȱ���ACF������CE��BF���轻��ΪM�����M��Ϊ��ABC�ķ����㣮��˵���������������ݣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com