
【题目】某商店周年庆,印刷了1000张奖券,其中印有老虎图案的有10张,每张奖金1000元,印有羊图案的有50张,每张奖金100元,印有鸡图案的有100张,每张奖金20元,印有兔子图案的有400张,每张奖金2元,其余印有花朵图案但无奖金,从中任意抽取一张,请解答下列问题:
(1)获得1000元奖金的概率是多少?
(2)获得奖金的概率是多少?
(3)若要使获得2元奖金的概率为![]() ,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券?
,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券?
【答案】(1)![]() ;(2)
;(2)![]() ;(3) 需要将600张印有花朵图案的奖券换为印有兔子图案的奖券
;(3) 需要将600张印有花朵图案的奖券换为印有兔子图案的奖券
【解析】
(1)由10000张奖券中有10张印有老虎图案,每张奖金1000元,再根据概率公式即可得出答案;
(2)先求出能获得奖金的奖票张数,再根据概率公式即可得出答案;
(3)设需要将x张印有花朵图案的奖券换为印有兔子图案的奖券,根据概率公式列出算式,求出x的值即可.
(1)获得1000元奖金的概率是![]() ;
;
(2)由题意知:能获得奖金的奖票有10+50+100+400=560张,获得奖金的概率是:![]() ;
;
(3)设需要将x张印有花朵图案的奖券换为印有兔子图案的奖券,根据题意得:
![]() ,
,
解得:x=600,
答:需要将600张印有花朵图案的奖券换为印有兔子图案的奖券.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( ) 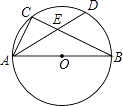
A.2.5
B.2.8
C.3
D.3.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l ,则B、E1两点之间的距离为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到章丘某旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 景点离小明家180千米 B. 小明到家的时间为17点
C. 返程的速度为60千米每小时 D. 10点至14点,汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为![]() .
.

(1)图①中打包带的总长![]() =________.
=________.
图②中打包带的总长![]() =________.
=________.
(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较 ![]() 的大小.)
的大小.)
(3)若b=40且a为正整数,在数轴上表示数![]() 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.在数轴上若点A、B分别表示有理数a、b ,在数轴上A、B两点之间的距离AB=| a-b | .结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示﹣3和2的两点之间的距离是_____;数轴上表示 x 和 -3 两点之间的距离是_____;
(2)若a表示一个有理数,则|a+4|+|a﹣2|有最小值吗?若有,请求出最小值;若没有,请说明理由;
(3)当a =_____时,|a+4|+|a﹣1|+|a﹣2|的值最小,最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac
其中正确的结论的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有 A、B 两点,所表示的有理数分别为 a、b,已知 AB=12,原点 O 是线段AB 上的一点,且 OA=2OB.
![]()
(1)求a,b;
(2)若动点 P,Q 分别从 A,B 同时出发,向右运动,点 P 的速度为每秒 2 个单位长度,点 Q 的速度为每秒 1 个单位长度,设运动时间为 t 秒,当点 P 与点 Q 重合时,P,Q 两点停止运动.
①当 t 为何值时,2OPOQ=4;
②当点 P 到达点 O 时,动点 M 从点 O 出发,以每秒 3 个单位长度的速度也向右运动,当点 M 追上点 Q 后立即返回,以同样的速度向点 P 运动,遇到点 P 后再立即返回,以同样的速度向点 Q 运动,如此往返,直到点 P,Q 停止时,点 M 也停止运动,求在此过程中点 M 行驶的总路程,并直接写出点 M 最后位置在数轴上所对应的有理数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com