
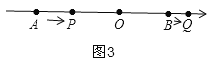
【题目】如图,数轴上有 A、B 两点,所表示的有理数分别为 a、b,已知 AB=12,原点 O 是线段AB 上的一点,且 OA=2OB.
![]()
(1)求a,b;
(2)若动点 P,Q 分别从 A,B 同时出发,向右运动,点 P 的速度为每秒 2 个单位长度,点 Q 的速度为每秒 1 个单位长度,设运动时间为 t 秒,当点 P 与点 Q 重合时,P,Q 两点停止运动.
①当 t 为何值时,2OPOQ=4;
②当点 P 到达点 O 时,动点 M 从点 O 出发,以每秒 3 个单位长度的速度也向右运动,当点 M 追上点 Q 后立即返回,以同样的速度向点 P 运动,遇到点 P 后再立即返回,以同样的速度向点 Q 运动,如此往返,直到点 P,Q 停止时,点 M 也停止运动,求在此过程中点 M 行驶的总路程,并直接写出点 M 最后位置在数轴上所对应的有理数.
【答案】(1)a=-8,b=4;(2)①当 t 为 1.6 秒或 8 秒时,2OP-OQ=4;②点 M 行驶的总路程为 24 和点 M 最后位置在数轴上对应的实数为16.
【解析】
(1)由AO=2OB可知,将12平均分成三份,AO占两份为8,OB占一份为4,由图可知,A在原点的左边,B在原点的右边,从而得出结论;
(2)①分两种情况:点P在原点的左侧和右侧时,OP表示的代数式不同,OQ=4+t,分别代入2OP﹣OQ=4列式即可求出t的值;
②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为t秒,列式为t(2﹣1)=8,解出即可解决问题.
(1)∵AB=12,AO=2OB,∴AO=8,OB=4,∴A点所表示的实数为﹣8,B点所表示的实数为4,∴a=﹣8,b=4.
故答案为:﹣8;4;
(2)①当0<t≤4时,如图3,AP=2t,OP=8﹣2t,BQ=t,OQ=4+t.
∵2OP﹣OQ=4,∴2(8﹣2t)﹣(4+t)=4,t=![]() =1.6;
=1.6;
当点P与点Q重合时,如图4,2t=12+t,t=12;
当4<t<12时,如图5,OP=2t﹣8,OQ=4+t,则2(2t﹣8)﹣(4+t)=4,t=8.

综上所述:当t为1.6秒或8秒时,2OP﹣OQ=4;
②当点P到达点O时,8÷2=4,此时,OQ=4+t=8,即点Q所表示的实数为8,如图6,设点M运动的时间为t秒,由题意得:2t﹣t=8,t=8,此时,点P表示的实数为8×2=16,所以点M表示的实数也是16,∴点M行驶的总路程为:3×8=24.
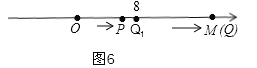
答:点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.


科目:初中数学 来源: 题型:
【题目】某商店周年庆,印刷了1000张奖券,其中印有老虎图案的有10张,每张奖金1000元,印有羊图案的有50张,每张奖金100元,印有鸡图案的有100张,每张奖金20元,印有兔子图案的有400张,每张奖金2元,其余印有花朵图案但无奖金,从中任意抽取一张,请解答下列问题:
(1)获得1000元奖金的概率是多少?
(2)获得奖金的概率是多少?
(3)若要使获得2元奖金的概率为![]() ,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券?
,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数![]() (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.

(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC. 
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数图象如图所示,根据图象可得: 
(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年某市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出不完整的统计表如下:
升学意向 | 省级示范高中 | 市级示范高中 | 一般高中 | 职业高中 | 其他 | 合计 |
人数 | 15 | 15 | 9 | 3 | m | |
百分比 | 25% | 25% | n | 5% | 100% |
请你根据统计表提供的信息解答下列问题:
(1)表中m的值为 ,n的值为 ;
(2)补全图7中的条形统计图;
(3)若该校九年级有学生500名,估计该校大约有多少名毕业生的升学意向是职业高中?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左面的几何体叫三棱柱,它有五个面,![]() 条棱,
条棱,![]() 个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
个顶点,中间和右边的几何体分别是四棱柱和五棱柱.

![]() 四棱柱有________个顶点,________条棱,________个面;
四棱柱有________个顶点,________条棱,________个面;
![]() 五棱柱有________个顶点,________条棱,________个面;
五棱柱有________个顶点,________条棱,________个面;
![]() 你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
![]() 棱柱有几个顶点,几条棱,几个面吗?
棱柱有几个顶点,几条棱,几个面吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,点
,点![]() 为数轴上一动点.
为数轴上一动点.
(1) AB的距离是 .
(2) ①若点![]() 到点
到点![]() 的距离比到点
的距离比到点![]() 的距离大1,点
的距离大1,点![]() 对应的数为 .
对应的数为 .
②若点![]() 其对应的数为
其对应的数为![]() ,数轴上是否存在点
,数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)当点![]() 以每秒钟
以每秒钟![]() 个单位长度从原点
个单位长度从原点![]() 向右运动时,点
向右运动时,点![]() 以每秒钟
以每秒钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向左运动,点
向左运动,点![]() 以每秒钟
以每秒钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向右运动,问它们同时出发 秒钟时,
向右运动,问它们同时出发 秒钟时,![]() (直接写出答案即可).
(直接写出答案即可).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查方式合适的是( )
A. 为了了解外地游客对岳阳楼新景区的感受,小华利用周日在汴河街随机采访了![]() 名武汉游客
名武汉游客
B. 为了了解全校学生用于做数学作业的时间,小民同学在网上通过![]() 向
向![]() 位好友做了调查
位好友做了调查
C. 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式
D. 为了了解全国青少年儿童在阳光体育运动启动后的睡眠时间,统计人员采用了普查的方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com