练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线l上摆放着两块大小相同的直角三角形△ABC和△ECD，∠ACB=∠DCE=90°，且BC=CE=3，AC=CD=4，将△ECD绕点C逆时针旋转到△E1CD1位置，且D1E1∥l ，则B、E1两点之间的距离为___________.

    【答案】

    【解析】过E1作E1F⊥BC，D1E1 与AC交于点O，如图：

    ∵D1E1∥l，∠DCE=90°，∴CO为△E1CD1的高，在△E1CD1中，BC=CE=CE1=3，AC=CD=CD1=4，

    根据勾股定理得：D1E1=5，根据直角三角形面积公式CE1CD1=D1E1CO，解得：CO==E1F，

    在Rt△CE1F中，利用勾股定理得：，解得：CF=，∴BF=BC-CF=3-=，

    在Rt△BFE1中，利用勾股定理得：，解得：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（ ）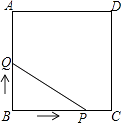

    A.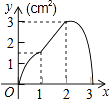
    B.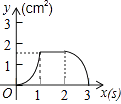
    C.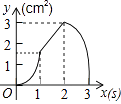
    D.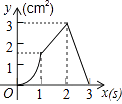

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点E在△ABC内，∠ABC=∠EBD=α，∠ACB=∠EDB=60°，∠AEB=150°，∠BEC=90°．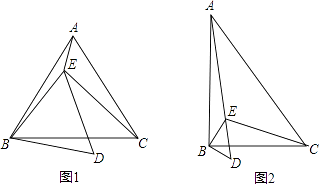
    （1）当α=60°时（如图1）， ①判断△ABC的形状，并说明理由；
    ②求证：BD= AE；
    （2）当α=90°时（如图2），求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工程，甲工程队单独做40天完成，若乙工程队单独做30天后，甲、乙两工程队再合作20天完成。

    （1）（5分）求乙工程队单独做需要多少天完成？

    （2）（4分）将工程分两部分，甲做其中一部分用了x天，乙做另一部分用了y天，其中x、y均为正整数，且x<15，y<70，求x、y.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．

    （1）图②中的大正方形的边长为　 　；阴影部分的正方形的边长为　 　；

    （2）请用两种方式表示图②中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一位射击运动员在10次射击训练中，命中靶的环数如图． 请你根据图表，完成下列问题：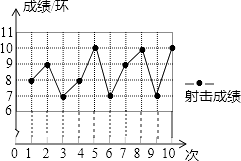

    （1）补充完成下面成绩表单的填写：

    射击序次

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    成绩/环

    8

    10

    7

    9

    10

    7

    10


    （2）求该运动员这10次射击训练的平均成绩．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店周年庆,印刷了1000张奖券,其中印有老虎图案的有10张,每张奖金1000元,印有羊图案的有50张,每张奖金100元,印有鸡图案的有100张,每张奖金20元,印有兔子图案的有400张,每张奖金2元,其余印有花朵图案但无奖金,从中任意抽取一张,请解答下列问题：

    (1)获得1000元奖金的概率是多少?

    (2)获得奖金的概率是多少?

    (3)若要使获得2元奖金的概率为,则需要将多少张印有花朵图案的奖券换为印有兔子图案的奖券?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y＝(x＞0)和y＝－(x＞0)的图象于A，B两点，C是y轴上任意一点，则△ABC的面积为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC．

    （1）作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1 ， （只画出图形）．
    （2）作出△ABC关于原点O成中心对称的△A2B2C2 ， （只画出图形），写出B2和C2的坐标．

    查看答案和解析>>

    同步练习册答案