
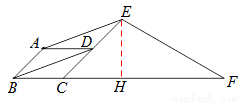
如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°, AB=2.
求CF的长.

2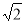 +2
+2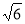 .
.
【解析】
试题分析:易证四边形ABDE是平行四边形,则AB=DE=CD,过点E作EH⊥BF于点H,解等腰直角三角形CEH得EH=CH=2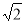 ,解FH=2
,解FH=2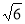 ,从而得CF=2
,从而得CF=2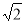 +2
+2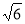 .
.
试题解析:∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC.
∵AE∥BD,∴四边形ABDE是平行四边形.
∴AB=DE=CD,即D为CE中点.
∵AB=2,∴CE=4.
又∵AB∥CD,∴∠ECF=∠ABC=45°.
如图,过点E作EH⊥BF于点H,
∵CE=4,∠ECF=45°,∴EH=CH=2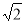 .
.
∵∠EFC=30°,∴ FH=2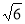 ,∴ CF=2
,∴ CF=2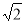 +2
+2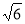 .
.
考点:1.平行四边形的判定与性质;2.含30度角直角三角形的性质;3.等腰直角三角形的性质.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
如图,抛物线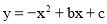 经过A
经过A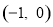 、C(0,4)两点,与x轴的另一交点是B.
、C(0,4)两点,与x轴的另一交点是B.
(1)求抛物线的解析式;
(2)若点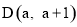 在第一象限的抛物线上,求点D关于直线BC的对称点
在第一象限的抛物线上,求点D关于直线BC的对称点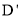 的坐标;
的坐标;
(3)在(2)的条件下,过点D作DE⊥BC于点E,反比例函数 的图象经过点E,点
的图象经过点E,点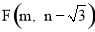 在此反比例函数图象上,求
在此反比例函数图象上,求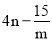 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:选择题
国家统计局公布了2014年1月的居民消费价格指数(CPI),16个省市CPI同比涨幅超过全国平均水平,其中7个省市的涨幅如下表:
地区 | 北京 | 广东 | 上海 | 浙江 | 福建 | 云南 | 湖北 |
同比涨幅(﹪) | 3.3 | 3.3 | 3.0 | 2.8[ | 2.8 | 2.8 | 2.3 |
则这组数据的众数和中位数分别是( )
A.2.8,2.8 B.2.8,2.9 C.3.3,2.8 D.2.8,3.0
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
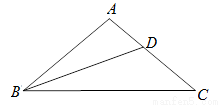
问题:在△ABC中,AB=AC,∠A=100°,BD为∠B 的平分线,探究AD、BD、BC之间的数量关系.
请你完成下列探究过程:
(1)观察图形,猜想AD、BD、BC之间的数量关系为 .
(2)在对(1)中的猜想进行证明时,当推出∠ABC=∠C=40°后,可进一步推出∠ABD=∠DBC= 度.
(3)为了使同学们顺利地解答本题(1)中的猜想,小强同学提供了一种探究的思路:在BC上截取BE=BD,连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路,画出图形,在此基础上对(1)中的猜想加以证明.也可以选用其它的方法证明你的猜想.
查看答案和解析>>
科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:选择题
在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
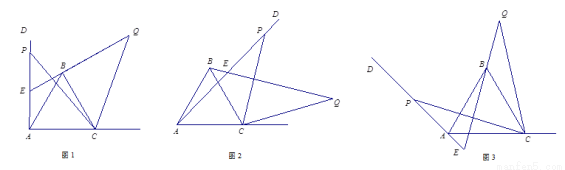
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com