
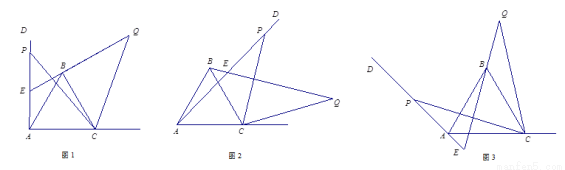
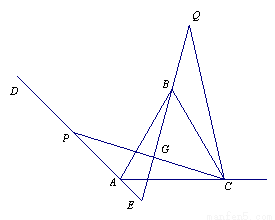
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
(1) 60°;(2) 60°,证明见解析;(3)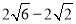 .
.
【解析】
试题分析:(1)由△ACP≌△BCQ得到∠APC=∠Q,根据圆周角定理,点P、E、C、Q 四点共圆,所以∠QEP=∠PCQ=6O°.
(2)同(1)可得.
(3)证明△GBC为等腰直角三角形,即可根据等腰直角三角形的性质求得BQ的长.
(1)60°.
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
又由题意可知,CP=CQ,∠PCQ=6O°,
∴∠ACP=∠BCQ.
∴ △ACP≌△BCQ.
∴ ∠APC=∠Q.
∴点P、E、C、Q 四点共圆.
∴∠QEP=∠PCQ=6O°.
(2)60°.以∠DAC是锐角为例证明如下:
∵ △ABC是等边三角形,
∴AC=BC,∠ACB=60°.
又由题意可知,CP=CQ,∠PCQ=6O°,
∴∠ACP=∠BCQ.
∴ △ACP≌△BCQ.
∴ ∠APC=∠Q.
∴点P、E、C、Q 四点共圆.
∴∠QEP=∠PCQ=6O°.
(3)设PC与BQ交于点G,
由题意可求,∠APC=30°,∠PCB=45°.
又由(2)可证 ∠QEP=60°.
∴可证QE垂直平分PC,
∴△GBC为等腰直角三角形.
∵AC=4,
∴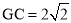 ,
,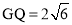
∴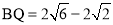 .
.
考点:1.线动旋转问题;2.等边三角形的性质;3.全等三角形的判定和性质;4.圆周角定理;5.等腰直角三角形的判定和性质.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源:2014年北京市怀柔区中考一模数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°, AB=2.
求CF的长.

查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
在一个口袋中,装有质地、大小均相同、颜色不同的红球3个,蓝球4个,黄球5个,现在随机抽取一个球是红球的概率是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
如图,已知AB∥CD,BC平分∠ABE,∠C= ,则∠BED 的度数是( )
,则∠BED 的度数是( )
A.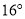 B.
B. C.
C.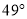 D.
D.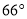
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:解答题
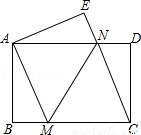
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,且CD=4,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源:2014年北京市东城区中考一模数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第5次碰到矩形的边时,点P的坐标为 ;当点P第2014次碰到矩形的边时,点P的坐标为____________.

查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
平行四边形的对角线一定具有的性质是( )
A.相等 B.互相平分 C.互相垂直 D.互相垂直且相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com